KEMOMETRIA '98
program és összefoglalók
|
Okt. 7. Szerda délután 14 00 - 18 45
Klasszikus kemometria, oktatása, eloszlások, hipotézisvizsgálat,
variancia-analízis, stb.
|
| 14 00 - 14 10 |
Köszöntő |
| 14 10 - 15 00 |
Szepesvári Pál: A kemometria oktatásáról (A tervezett tankönyv szinopszisa) |
| 15 00 - 15 25 |
Somogyi András: Konfidencia-tartomány számítása
likelihood ratio módszerrel |
| 15 25 - 15 55 |
Lengyel Attila, Paksy László, Bánhidi
Olivér: Nem-paraméteres módszerek alkalmazása környezeti adatok elemzésére.
Eloszlások vizsgálata |
| 15 55 - 16 15 |
Szünet |
| 16 15 - 17 00 |
Kemény Sándor, Sarkadi Ádám, Brumbauer Anikó: EEG
adatok feldolgozása varianciaanalízissel - hogy hogy kell vigyázni! |
| 17 00 - 17 30 |
Paksy László, Lengyel Attila, Bánhidi
Olivér: Nemparaméteres módszerek alkalmazása környezeti adatok trendjének
vizsgálatára. |
| 17 30 - 18 00 |
Raisz Péter, Raisz Iván: Vízfolyás szennyezettségének
vizsgálata statisztikai módszerekkel |
|
Okt. 8 Csütörtök délelőtt: 8 30 - 13 00
Többváltozós módszerek, Főkomponenselemzés, mesterséges
neuronhálók, alkalmazások
|
| 8 30 - 9 30 |
Hlavay József: Analitikai módsz-erek validálása.
Megfelelés a célnak |
| 9 30 - 9 55 |
Héberger Károly, Keszler Ágnes: Növényolajoxidációban
képződő hidroperoxidok bomlása során mért jellemzők főkomponenselemzése |
| 9 55 - 10 20 |
Borosy András és Héberger Károly:
Kemometriai módszerek összehasonlítása győkaddíciós reakciók aktiválási
para-métereinek előrebecslésére |
| 10 20 - 10 45 |
Marsi István, Viskolz Béla és Seres
László: A csoportadditivitás-módszer alkil gyökökre való alkalmazhatóságának
vizs-gálata ab initio adatok felhhasználásával; Egy többváltozós
feladat kezelése |
| 10 45 - 11 15 |
Szünet |
| 11 15 - 11 45 |
Rajkó Róbert: A párkorrelációs módszer
alkalmazása gyors nedvesség-tartalom meghatározó módszer fejlesztésénél |
| 11 45 - 12 15 |
Rajkó Róbert és Héberger Károly: A párkorrelációs
módszer MS Excel VBA változata új teszt statisztikákkal |
| 12 15 - 13 00 |
Pap Tamás, Pápai Zsuzsa:
Folyadékkromatográfiás elemzések optimálása kísérlettervezéssel,
szimplex módszerrel és csúcsalakelemzéssel |
|
Okt. 8 Csütörtök, délután
Tanulmányi kirándulás
A kemometria helyzete, jövője megbeszélés
|
|
Okt. 9. Péntek: 9 00 - 16 00
Szerkezet - hatás összefüggések és a kemometria helyzete
|
| 9 00 - 9 45 |
Horvay György: Szenzorok szelektivitása |
| 9 45 - 10 15 |
Lukovits István: Szerkezeti izomerek
képleteinek generálása számítógéppel |
| 10 15 - 10 45 |
Lukovits István és Kálmán Erika:
Kvantitatív hatás-szerkezet összefüggések korróziós inhibítorok
sorában |
| 10 45 - 11 10 |
Szünet |
| 11 10 - 11 35 |
Kutsán Gy., Bundula R., Körtvélyesi
T., Rauscher Á.: Acetilén-származékok korróziós inhibíciós aktivitás-szerkezet
összefüggése |
| 11 35 - 12 30 |
A kemometria helyzete, jövője. A kerekasztal
megbeszélés vitaindítója: Héberger Károly |
| 12 30 - 14 00 |
Ebéd |
| 14 00 - 16 00 |
Szakcsoport ülés, a megbeszélés folytatása, az 1999 februári
analitikai ankét műsorának, az egyesületi tisztújításnak és a szakcsoport
nemzetközi kapcsolatainak megbeszélése |
KONFIDENCIA-TARTOMÁNY SZÁMÍTÁSA LIKELIHOOD RATIO MÓDSZERREL
Somogyi András
ELTE TTK Kémiai Tanszékcsoport
Budapest
Többváltozós, nemlineáris paraméterbecsléssel meghatározott
paraméterek konfidencia-tartományát leggyakrabban annak szimmetrikus közelítésével szokás
számítani. A likelihood ratio módszer ezt a közelítést nem alkalmazza,
így segítségével a konfidencia-tarományok finomabb részletei is feltárhatók.
Az előadás enneka módszernek a bemutatásával és egy alkalmazási
példával foglalkozik.
A módszer működése, és a konfidencia-taromány egy hatékony számítási módszere egyszerűen
bemutatható egyetlen paraméter becslése, azaz egydimenziós tartomány
esetére. A számítási módszer kiterjeszthető több paraméter többdimenziós
tartományának becslésére is. Első lépésben a kétdimenziós kiterjesztésről,
és a tartomány ellipszis alakja által okozott probléma megoldásáról
lesz szó, majd ennek általánosításáról több dimenzióba.
Végezetül egy egyszerű kémiai probléma vizsgálatán bemutatásra kerül a likelihood ratio
módszerrel meghatározott konfidencia-tartomány, és annak összehasonlítása
a szimmetrikus közelítéssel.
VÍZFOLYÁS SZENNYEZETTSÉGÉNEK
VIZSGÁLATA STATISZTIKAI MÓDSZEREKKEL
Raisz Péter(1), Raisz Iván(2)
(1) Miskolci Egyetem Matematikai Intézet
3515 Miskolc-Egyetemváros, E-mail:
(2) Miskolci Egyetem Kémiai Intézet Fizikai
Kémiai Tanszék
3515 Miskolc-Egyetemváros, E-mail: fkmraisz@gold.uni-miskolc.hu
A veszélyeztetett vízbázisok védelme program keretében
vizsgáltuk Sirok és térsége környezetében a Tarna vizének szennyezettségét.
A szennyezettség vizsgálatát az indokolta, hogy a tríciumos vizsgálatok
szerint szerepe van a felszíni vízbeszűrődésnek is a termelt víz
szennyezettségében.
A vizsgálatokhoz felhasználtuk az elmult években a
felszíni vizek analízisekor nyert adatokat.
A felhasznált idősorok sok esetben hézagosak, az egymással konkuráló,
vagy megerősítő sajátságok vizsgálatára nincs lehetőség. Ez különösen
érdekes lett volna az oldott oxigén tartalom, KOI és TOC együttes vizsgálatánál.
Mivel nem állt szándékunkban
az egyes konkrét szennyvízkibocsátók megnevezése ezért szorítkoztunk
a trendek vizsgálatára és a kiugró értékek jelzésére. Amikor egy-egy
komponensben kiugró értéket találtunk, azt csak egy azonos mintában
levő szintén kiugró, a trendbe nem
illő érték esetén tartottuk elfogadhatónak, ellenkező esetben mérési
hibaként a következtetések levonásakor figyelmen kívül hagytuk.
A nem ellenőrzött szennyezések
felderítésére szükségesnek tartjuk a szennyező komponens
tömeg-, vagy ekvivalens áramát vizsgálni, mert ez ad lehetőséget
az anomáliák felderítésére. Ez alól csak az oldott oxigén tartalom
a kivétel, melyet a hőmérsékleti egybevetés és megfelelőség vizsgálatára
pillanatnyi koncentrációban is megadtunk.
Fentiekből arra a következtetésre
jutottunk, hogy a vizsgálatok akkor adnak lehetősget
az ismeretlen szennyezések és szennyezők felderítésére, ha a folyó
állapotát minden tekintetben leíró adatsorok állnak rendelkezésre
a vízfolyás több szelvényében.
EEG ADATOK FELDOLGOZÁSA VARIANCIA-ANALÍZISSEL - HOGY HOGY KELL VIGYÁZNI
Kemény Sándor(1), Sarkadi
Ádám(2), Brumbauer Anikó(1)
(1) Budapesti Műszaki Egyetem
(2) Richter Gedeon Vegyészeti Gyár Rt.
A munka célja az ischaemiás hypoxia kezelésére szolgáló
vegyület összehasonlító vizsgálata. Az ischaemiás
hypoxiát a nyaki verőér kétoldali leszorításával (BCO) modellezték,
állat-egyedenként egymás után hatszor. Az állatok állapotát fényfelvillanással
kiváltott EEG-jelek regisztrálásával követték nyomon. A mérést
a leszorításkor és az azt követő 10. és 20. percben végezték. Egy
állat három anyag (placebo, egy ismert gyógyszer és a vizsgálandó
vegyület) valamelyikét kapta a 3. BCO után.
A három faktor (BCO sorszám,
idő, vegyület) szerinti kereszt-osztályozás meglepő eredményeket
adott. Először úgy tűnt, hogy a vegyületek hatásában jelentős különbség
van a második 3 BCO alatt, méghozzá a vizsgálandó anyag javára. Az
első 3 BCO vizsgálatával viszont az derült ki, hogy a vegyületek hatásában
már akkor is jelentős különbség van, amikor meg sem kapták még
az anyagot.
A kísérletek elvégzésének
rendjét átgondolva egyértelmű volt, hogy a hibák hagyományos
és egyszerű varianciaanalízis követelte függetlensége nem áll fönn:
ún. "repeated measures" típusú tervről van szó, amely közelítőleg
"split-plot" tervként is kezelhető. A 24 EEG-paraméter elemzésének
egyesítésével, a hatások kimutathatóságának erősítésére
omnibusz-próbát alkalmaztunk. Ezzel egyértelműen igazoltuk, hogy a
vegyületek hatásában van különbség. Fontos tapasztalat, hogy
a vizsgált vegyülettel kezelve az állatokat az egyedenkénti ingadozás
jóval kisebb.
NEM-PARAMÉTERES
MÓDSZEREK ALKALMAZÁSA KÖRNYEZETI ADATOK ELEMZÉSÉRE. ELOSZLÁSOK VIZSGÁLATA
Lengyel Attila(1), Paksy László(2),
Bánhidi Olivér(3)
(1) Miskolci Egyetem, Kémiai Intézet,Analitikai
Kémiai Tanszék
H-3515 Miskolc-Egyetemváros, e-mail: akmla@gold.uni-miskolc.hu
(2) Miskolci Egyetem, Kémiai
Intézet, Analitikai Kémiai Tanszék
Miskolc, H-3515 e-mail: akmpl@gold.uni-miskolc.hu,
(3) Metalcontrol Kft.
3540 Miskolc,Vasgyári u 43., e-mail: qjojade@gold.uni-miskolc.hu
A környezet állapotának
vizsgálata során általában azt kell felderíteni, hogy valamely ismert
jelenség (például az ózon képződése a közlekedés által terhelt
városi levegőben, vagy a nitrát koncentrációja felszíni vízfolyásokban)
kimutatható-e vagy sem, és ha igen, milyen mértékben felelős a környezet
szennyezettségéért.
A nyert adatok elemzésével ezekre a kérdésekre úgy
kell válaszolnunk, hogy a hatások valószínűségét
is becsülni tudjuk.
A korábbi vizsgálataink alapján nyilvánvaló, hogy
az eloszlások csak a legritkább esetben normál-eloszlások, következésképpen
a paraméteres módszerek alkalmatlanok a statisztikai vizsgálatra.
Ugyancsak becsülhetetlen
az eloszlás milyensége; nem tudható előre, hogy milyen eloszlású
halmazra számíthatunk.
Fentiek miatt csak a nem-paraméteres módszerek használthatók
a tesztekhez és a hipotézis vizsgálatokhoz.
Az előadásban példákat
mutatunk be a nem-paraméteres módszerekre, alkalmazva azokat légszennyezés
és felszíni víz szennyezéseinak vizsgálatára. Többek között bemutatjuk
a
-
Khi-tesztet az eloszlás normál/vagy nem normális voltának
eldöntésére, valamint
-
Wilcoxon és
-
Kolmogorov-Szmirnov tesztet két eloszlás azonosságának
kimutatására.
Ugyancsak bemutatjuk a Rank-korrelációs vizsgálataink
eredményét ugyanezen vizsgálati adatokra.
[1]
L.Paksy, A.Lengyel, O.Bánhidi : Microchem. J. 59,258-268 (1998)
[2]
Vincze,I., Varbonova, M.: Nemparaméteres matematikai statisztika, Elmélet
és alkalmazások. Akadémiai Kiadó, Bp. 1993
NEMPARAMÉTERES MÓDSZEREK
ALKALMAZÁSA KÖRNYEZETI ADATOK TRENDJÉNEK VIZSGÁLATÁRA
Paksy László(1), Lengyel Attila(2),
Bánhidi Olivér(3)
(1) Miskolci Egyetem, Kémiai Intézet, Analitikai
Kémiai Tanszék
3515 Miskolc-Egyetemváros, e-mail: akmpl@
gold.uni-miskolc.hu,
(2) Miskolci Egyetem, Kémiai Intézet,Analitikai
Kémiai Tanszék
3515 Miskolc, e-mail: akmla@
gold.uni-miskolc.hu
(3) Metalcontrol Kft.
3540 Miskolc,Vasgyári u 43., e-mail: qjojade@
gold.uni-miskolc.hu
A környezetben végbemenő
változások leírása az alapja környezetünk megismerésének,
a megfelelő környezetvédelem kialakításának. A rendelkezésre álló
adatsorok alapján a trendet illetően is válaszolnuk kell a következő
kérdésekre:
1. A vizsgált, a környezet
állapotát, a végbemenő folyamatokat leiró fizikai, kémiai paraméterek
értékei mutatnak-e, különböző időszakokat vizsgálva változást
?
2. A változásoknak van-e
trendje, és ha igen, a trend jellege milyen, pl. különböző időszakokat
összehasonlítva azonos, vagy véletlenszerű?
3. Azonos vagy különböző
környezetre vonatkozóan vizsgált paraméterek adatsorai hasonló változást,
trendet mutatnak-e?
4. Bizonyítható-e a trend kialakulásában valamilyen
fizikai, kémiai környezeti paraméter hatása ?
Figyelembe véve, hogy ezen adatsorok igen sok esetben nem
a Gauss eloszlást követik [1]
, a fenti kérdésekre nemparaméteres statisztikai próbák segítségével
adhatunk választ [2]
.
1. A különböző időszakokra
mért adatsorokat a Wilcoxon rangösszegpróbával hasonlíthatjuk
össze, az adatsorok közötti D különbségre
pontbecslést végezhetünk a mediánok segítségével.
2. Különböző időszakokra
(pl. egy napon belül valamely időpontra vonatkozóan, vagy magára az
egész napra vonatkozóan ) a rank-korrelációval vizsgálhatjuk a trendet.
Kellően nagyszámú adat esetén (ami pl. monitoring állomásoknál rendelkezésre
áll), t-próbával határozhatjuk meg a korreláció szignifikáns voltát.
3. A trendek különböző
összehasonlítandó időszak-sorozatokra vonatkozó véletlen fellépésére
vonatkozóan a Wald-Wolfowitz sorozatpróbát alkalmazhatjuk.
4. Az adatsorok időbeli
változásának hasonlóságát, valamint
5. a környezeti paraméterek hatását is rank korrelációval
lehet statisztikusan vizsgálni.
A feladat jellegétől függően
más nemparaméteres statisztikai próbák [
2] elvégzése is szükséges lehet.
Fentiek szemléltetésére gyakorlati példákat ismertetünk
Miskolc város levegő-tisztasági és a Sajó folyó szervetlen szennyező
elemeinek mért adatai alapján és kemometriailag értelmezzük az említett
statisztikai próbák eredményeit (pl. a trend természetes vagy mesterséges/antropogén
hatást tükröző voltát illetően
).
[1]
L.Paksy, A.Lengyel, O.Bánhidi : Microchem. J. 59,258-268 (1998)
[2]
Vincze,I., Varbonova, M.: Nemparaméteres matematikai statisztika, Elmélet
és alkalmazások. Akadémiai Kiadó, Bp. 1993
A PÁRKORRELÁCIÓS
MÓDSZER ALKALMAZÁSA GYORS NEDVESSÉGTARTALOM MEGHATÁROZÓ MÓDSZER FEJLESZTÉSÉNÉL
Rajkó Róbert
JATE Szegedi Élelmiszeripari
Főiskolai Kar,
Szegedi Felsőoktatási
Szövetség Tagintézmény
Élelmiszeripari
Műveletek és Környezettechnika Tanszék
6724 Szeged, Mars tér 7., levélcím: 6701 Szeged,
Pf. 433.
Tel.: (62)456-030, Fax: (62)456-034, E-mail: rajko@sol.cc.u-szeged.hu
Az irodalomban megjelent mikrohullámú kezeléssel megvalósított
gyors nedvességtartalom meghatározást a
szójababban lévő antinutritív anyagok csökkentésére irányuló
mikrohullámú hőkezelés során alkalmaztuk. Az irodalomban megjelent
adatok matematikai statisztikai elemzésével eltérő következtetésre
jutottunk, mint az idézett tanulmány szerzői: az y = a exp(bx) exponenciális függvénykapcsolat helyett az y = a xc exp(b x) összefüggést javasoljuk. Az
új összefüggést alkalmazva az 1,5 percig tartó mikrohullámú kezelést
találtuk a legjobban alkalmazhatónak a nedvességtartalom
pontos előrebecsléséhez.
A vizsgálatok második szakaszában vörösárú nedvességtartalom
meghatározására irányuló kísérleteket végeztünk. összehasonlítottuk
a mikrohullámú eredményeket 2 inframérleggel kapottal. A száradási
sebességgörbék származtatását nem numerikus deriválással, hanem
a sokkal stabilabb és pontosabb eredményt szolgáltató simító spline
alkalmazásával valósítottuk meg.
A mérésekhez Labotron 500 vákuumozható mikrohullámú
berendezést alkalmaztunk impulzus-szerű
üzemmódban. A kezelések idejét szisztematikusan változtattuk.
A kísérleteket elvégeztük légköri nyomáson és vákuum alkalmazása
mellett is.
Az eredmények kiértékelése során fel kellett használnunk
a pár-korrelációs módszert, hogy szignifikáns
különbséget tehessünk a kezelési idők, valamint a felhasznált összefüggések
és regressziós módszerek között. Következtetéseink alapján ajánlást
teszünk a nedvességtartalmat legjobban
előrebecslő eljárás gyakorlati kivitelezésére.
A kutatásokat az OTKA (F 025287) támogatásával végeztük.
A PÁR-KORRELÁCIÓS MÓDSZER MS EXCEL VBA VÁLTOZATA ÚJ TESZT-STATISZTIKÁKKAL
Rajkó Róbert(1) , Héberger
Károly(2)
(1) JATE Szegedi Élelmiszeripari Főiskolai Kar, Szegedi Felsőoktatási Szövetség Tagintézmény,
Élelmiszeripari Műveletek és Környezettechnika Tanszék
6724 Szeged, Mars tér 7. levélcím: 6701 Szeged,
Pf. 433.
Tel.: (62) 456 030, Fax: (62) 456 034, E-mail: rajko@sol.cc.u-szeged.hu
(2) Magyar Tudományos Akadémia Kémiai
Kutatóközpont, Kémiai Intézet,
1025 Budapest II., Pusztaszeri út 59-67. levélcím:
1525 Budapest, Pf. 17.
Tel.: (1) 325 79 00/347, Fax: (1) 325 75 54, E-mail:
heberger@cric.chemres.hu
A klasszikus modellépítő,
változó-kiválasztási algoritmusok hiányosságainak pótlására, a
közelmúltban dolgoztunk ki egy új eljárást [1]. A pár-korrelációs
módszer (PCM) nemparaméteres, az irodalomban ismert módszerektől eltérően
nem az előrebecslési jóság segítségével épít modellt. Ez
a módszer még statisztikailag egyenértékű
(annak tűnő) változók megkülönböztetésére is alkalmas. A módszer
azonban csak megfelelő szelekciós kritérium esetén használható, csak
akkor tudja megmondani, hogy a két változó különbsége szignifikáns-e.
Az előadásban a közelmúltban
született eredményeinkről számolunk be. Jól használható és kényelmesen
kezelhető programot fejlesztettünk a már igen elterjedt MS
Excel V5.0-7.0 táblázatkezelő Visual
Basic for Application (VBA) fejlesztői
környezet felhasználásával. A programmal
különböző próbastatisztikák kipróbálására, alkalmazására
és eredményeik összehasonlítására van lehetőség.
Az alábbi próbastatisztikákat építettük a programba:
-
feltételes egzakt próba (Fisher-féle egzakt teszt),
-
nemparaméteres McNemar próba,
-
Khi-négyzet próba,
-
Williams féle t próba.
A pár-korrelációs módszer
általánosítása kettőnél több változó esetére újabb matematikai
statisztikai problémákat vet fel, melyek egyszerűbb megoldásait az
említett programba illesztettük,
előadásunkban ezekre is kitérünk.
A változók kiválasztására szolgáló módszerek:
-
a győzelmek száma szerinti
egyszerű sorbarendezés alapján.
-
a győzelmek és vereségek
különbsége szerinti sorrend alapján.
-
a győzelmek szignifikancia
szintjeinek összege szerint.
[1] K. Héberger and R. Rajkó: Discrimination of statistically
equivalent variables in quantitative structure-activity relationships.
In Quantitative Structure-Activity Relationships (QSAR) in Environmental
Sciences-VII, Ed. Fei Chen & Gerrit Schüürmann, SETAC Press,
1997, Ch. 29, 423-431
Jelen kutatást az OTKA T-016231 (H.K.), ill. F-025287
(R.R.) pályázata támogatta.
NÖVÉNYOLAJOXIDÁCIÓBAN
LÉVŐ HIDROPEROXIDOK BOMLÁSA SORÁN MÉRT JELLEMZŐK FŐKOMPONENSELEMZÉSE
Héberger Károly(*),
Keszler Ágnes
Magyar Tudományos Akadémia, Kémiai Kutatóközpont,
Kémiai Intézet,
1025 Budapest II. K Pusztaszeri út 59/67; 1525 Budapest
Pf. 17.
tel: 325 79 00; fax: 325 75 54; (*)email:
heberger@cric.chemres.hu
Növényolajoxidációban
lévő hidroperoxidok bomlását követtük szigorúan oxigénmentes
körülmények között, úgy, hogy mértük a peroxidszámot (jodometriásan)
az idő függvényében, a fényelnyelés értékeket l=232 és 268 nm-nél,
a para-anizidin
számot és az illékony termékek mennyiségét is, tömegspektriás detektálású
gázkromatográf segítségével, adalék
nélküli esetben valamint különböző adalékok alkalmazásával
is.
Az eredményeket mátrix
formába rendeztük és főkomponenselemzésnek vetettük
alá. Három főkomponens az adatokban lévő teljes variancia 91-98%-át
magyarázza meg. A mért jellemzők
és az adalékok hatása egymással szoros kapcsolatban van. A mért mennyiségek
közötti hasonlóságot az ún. loading
(főkomponenssúly) ábra, míg a különböző adalékok (ill. hatásuk)
hasonlóságat az ún. score ábra
mutatja.
A hidroperoxidok kezdeti bomlássebessége és
az illékony termékek (aldehidek) mennyisége egymással szorosan korreláló
mennyiségek. A fényelnyelés (abszorpció) értékei kiugrók. Egymáshoz
hasonlítanak ugyan, de jelentősen különböznek minden más mért mennyiségtől.
A para-anizidin szám különlegesen viselkedik, viszonya, hasonlósága
a többi változóhoz változik a hidroperoxidbomlás folyamán, ezért
felhasználható a kinetika követésére.
A legtöbb adalék hatása
hasonlít egymáshoz, bár két kiugró értéket itt is meg tudtunk figyelni.
A főkomponens-tengelyek forgatása egyik megállapítást sem változtatja
meg, ami a következtetések megalapozottságat sugallja. A számítások
megmutatják mely változók hordoznak azonos
és melyek eltérő információt, azaz mely jellemzőket
célszerű mérni az adalékok hatásásnak jellemzésére.
Az itt ismertetett munkát
az Európai Közösség (Copernicus program Ref. No CIPA-CT 94-0124) és
az Oszágos Tudományos Kutatási Alap ( szerződés száma. T016231) támogatta.
GYÖKADDÍCIÓS REAKCIÓK
AKTIVÁLÁSI PARAMÉTEREINEK ELŐREJELZÉSE
Borossy András Péter(1), Héberger Károly(2)
(1)BME, Vegyészmérnöki kar, Kémiai Informatika
T.sz.
Budapest, Gellért tér 4. 1119
Tel: 4632161, Fax: 4633953; E-mail: borossy@purple.inc.bme.hu
(2)MTA Kémiai Kutatóközpont, Kémiai Intézet
1025 Budapest, Pusztaszeri út 59-67.
Fax: 325 75 54; Tel: 325 79 00; E-mail: heberger@cric.chemres.hu
Gyökaddíciós reakciók:
R. + CH2=CXY ===> R-CH2-C.XY
{ahol R. alkilgyök, pl. (CH3)2C.OH; .CH2CN,
PhCH2.; .CH3, stb.
és X, Y: H, Ph, Me, CN, COOMe, OCOMe, OMe, CHO, stb.}
a kémia számos területén (pl. gyökös polimerizáció,
szerves szintézisek stb.) alapvető fontosságúak. Így ezen folyamatok
sebességi állandójának előrejelzése értelmes kutatási témának
tűnik. Az elmúlt évtizedek során a fenti reakciók sebességi állandója
ismertté vált [1-4].
A kísérleti adatok (sebességi állandó, reakcióhő,
ionizációs energia, elektronaffinitás) nagy száma [5] részletes statisztikai
elemzést is lehetővé tesz. Az előadás során a többszörös lineáris
regresszió, a főkomponens regresszió, a helyi súlyozott
regresszió és a visszafuttatásos mesterséges ideghálózatok
előrejelző képességét hasonlítjuk össze.
Mivel az alkalmazandó módszerek nagy része közvetett,
adathalmazunkat három részre (betanító, ellenőrző és előrejelző
halmazra) bontottuk, és kereszt ellenőrzést alkalmaztunk. A regressziók
reziduális hibája 4-5 kJ/mol-nak adódott.
A lineáris módszerek előrejelző képessége csekély,
ami arra utal, hogy az adatokban erőteljes nem-linearitás figyelhető
meg.
--------------------------------------------------------------------
[1] K. Münger and H. Fischer, Int. J. Chem. Kinet.,
17, 809 (1985)
[2] K. Héberger and H. Fischer, Int. J. Chem. Kinet., 25,
249 (1993)
[3] J. Q. Wu, I. Beranek, and H. Fischer, Helv. Chim. Acta,
78, 194 (1995)
[4] T. Zytowski and H. Fischer, J. Am. Chem. Soc., 118, 437
(1996)
[5] K. Héberger and H. Fischer, J. Chem. Soc. Perkin Trans.
2, (előkészületben)
A CSOPORTADDITIVITÁS-MÓDSZER
ALKIL GYÖKÖKRE VALÓ ALKALMAZHATÓSÁGÁNAK VIZSGÁLATA AB INITIO
ADATOK FELHASZNÁLÁSÁVAL.
EGY TÖBBVÁLTOZÓS FELADAT KEZELÉSE
Marsi István, Viskolcz Béla, Seres László
Szegedi Felsőoktatási
Szövetség
Juhász Gyula Tanárképző
Főiskola, Kémia Tanszék
6725 Szeged, Boldogasszony sgt. 6.
A csoportadditivitási elv alkalmazása - különösen
annak Sidney W. Benson és munkatársai által
megfogalmazott, könnyen alkalmazható változata - elősegítette a kémiai
reakciók termokémiai alapokon nyugvó tanulmányozását, nagymértékben
megkönnyítve a kísérleti munka tervezését és az eredmények
értékelését. A molekulák termokémiai adatainak becslésére szolgáló
csoportértékek nagyszámú vegyületre vonatkozó megbízható adatokra
támaszkodnak. Sajnos, nem ez a helyzet a gyökökre való alkalmazás
tekintetében, ahol - bár a csoportértékek származtatásához szükséges,
a legegyszerűbb alkilgyökökre vonatkozó
kísérleti adatok rendelkezésre állnak - a csoportadditivitási elv
alkalmazhatóságának semmilyen kísérleti bizonyítéka nem áll rendelkezésre.
),
C-(H)2(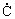 )(C), C-(H)(
)(C), C-(H)(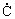 )(C)2,
C-(
)(C)2,
C-(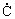 )(C)3
)(C)3 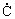 -(H)2(C),
-(H)2(C),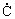 -(H)(C)2,
-(H)(C)2, 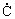 -(C)3
és 3 gauche kölcsönhatásra jellemző paraméter] származtatását.
Bebizonyosodott, hogy a feladat ebben
a formában elkerülhetetlenül fellépő identifikálhatósági
problémák miatt nem oldható meg. Az adatbázis bővítési lehetőségeit
illetve a modell paraméterei közötti (közelítő) azonosságot feltételező
egyszerűsítések bevezetését is megvizsgálva, kombinatorikus
módszerrel kiválasztottunk egy 12 csoportértékkel
jellemezhető, 30 alkil gyököt és 4 alkán molekulát magába
foglaló, a becsülhetőség szempontjából
optimális adatsort.
-(C)3
és 3 gauche kölcsönhatásra jellemző paraméter] származtatását.
Bebizonyosodott, hogy a feladat ebben
a formában elkerülhetetlenül fellépő identifikálhatósági
problémák miatt nem oldható meg. Az adatbázis bővítési lehetőségeit
illetve a modell paraméterei közötti (közelítő) azonosságot feltételező
egyszerűsítések bevezetését is megvizsgálva, kombinatorikus
módszerrel kiválasztottunk egy 12 csoportértékkel
jellemezhető, 30 alkil gyököt és 4 alkán molekulát magába
foglaló, a becsülhetőség szempontjából
optimális adatsort.
A regressziós feladat ezek
után megbízhatóan megoldható volt. Kimutattuk, hogy a várakozásnak
megfelelően a csoportadditivitás elve az (alkil) gyökökre is teljesül
és meghatároztuk a 12 csoportértéket. Utóbbiakra nézve mind a variancia,
mind a korreláltság mérsékelt. A kapott értékeket összevettük
az irodalmi adatokkal.
A KEMOMETRIA
OKTATÁSÁRÓL
Szepesváry Pál
ELTE Kémiai Tanszékcsoport, Budapest
Az előadás elsődleges
célja annak kifejtése, mit kellene vegyészeknek, vegyészmérnököknek,
természettudománnyal foglalkozóknak alapfokon kemometriából tanítani?
A kemometriát, felsőfokon, a rászorulóknak meg kell tanulniok, ilyen
vagy olyan módon, de most megkíséreljük
a minimum meghatározását. Szó esik arról is, milyen előismeretekre
kellene a kemometria oktatása során támaszkodni, nem szerencsés ugyanis,
ha a kemometria oktatása során tanítjuk meg azokat a matematikai, számítástechnikai
ismereteket, amelyeket korábban hatékonyabban lehetett volna elsajátí-tani.
Nem szerencsés az sem, ha a kemometriát "részletekben" tanítjuk, más
tárgyak keretében, olyan mértékben, amilyenben arra ott éppen szükség
van. Mindkét oktatási változat felületes tudást ad.
Az előadás másodlagos
célja annak elemzése, milyen intézkedésekre volna szükség
a kemometria oktatása érdekében.
A feszes tárgyalás kedvéért
kényszerűen szó esik a kemometria tartalmáról, kereteiről,
magyarán egy elfogadható definíciójáról, majd arról, hogyan függenek
össze egymással a kemo-metria diszciplinái. Erre a hatékony
tanulás miatt van szükség. Úgy gondoljuk ugyanis, hogy a kemometriának
a felhasználási területekhez igazodó, esetenkénti tárgyalása, bár
látszólag látványos, az ismétlések és a szertefutó nomenklatura
miatt sem nem hatékony, sem nem alapos.
A "hagyományos" kemometriai
ágak mellett szót kell ejteni és rokon diszciplinák és az "egyéb"
módszerek oktatási jelentőségéről, mint amilyenek az információ
elmélet, a mesterséges intelligencia, a mesterséges ideghálózatok,
a genetikus algoritmusok stb.
Az előadás második céljának
megfelelően olyan kérdéseket is érintünk, mint: mennyi idő kellene
az oktatáshoz, mikor kellene azt oktatni, hanyadik évben, milyen feltételeket
kellene biztosítani az egyetemeken, főiskolákon?
Érvelünk amellett, hogy egyetemeken szükség van arra,
hogy a kemometriai oktatás tanszékhez rendeltessék, hogy a matematikusokat megnyerjük a kemometriai oktatás igényeinek figyelembevételére,
hogy megkapjuk a szükséges órarendi engedményeket.
Ettől függetlenül szükség van alapfokú jegyzetre vagy
könyvre a sokváltozós kemometria
területéről, alapfokú (sokváltozós) kemometriai példatárra, PC-n,
vagy hálózaton át hozzáférhető kemometriai software-re, és az alapvető
kemometriai ismeretek WWW hozzáférhetőségére,
beleértve a példatárakat.
Az előadás végén megkíséreljük
számbavenenni szándékaink megvalósításának esélyeit.
SZERKEZETI IZOMEREK
KÉPLETEINEK GENERÁLÁSA SZÁMÍTÓGÉPPEL
Lukovits István
MTA, Kémiai Kutatóközpont
1525 Budapest, Pf. 17.
Mint ismeretes a molekulák szerkezeti képletei lényegében
színezett gráfok, az atomoknak a gráf pontjai, a kémiai kötéseknek
a gráf élei felelnek meg. A gráfok (szerkezeti képletek) azonosítására
az abszolut szelektív gráfinvariánsok (a gráf szerkezetétől
függő, de a pontok beszámozásától független számok) lennének a
legalkalmasabbak, de abszulut szelektív gráfinvariánst mind a
mai napig nem sikerült találni. A valóságban a gráfinvariánsokat
szerkezeti izomerek sorában számítják ki, annak eldöntésére, mennyire
szelektív az adott invariáns. Ekkor azonban az izomerek képleteinek
kimerítő és nem-redundáns generálása
a probléma. Ez utóbbi probléma a gráf pontjainak (az az a molekula
atomjainak) legcélszerűbb beszámozására vezethető vissza.
Bármely gráf egyértelműen leírható az A szomszédsági
mátrix segítségével, a mátrix i, j-edik eleme A(i,j) = 1, ha i és
j pontokat él köti össze, és A(i,j) = 0, minden más esetben. A tehát
szimmetrikus mátrix. A jobb felső része
aciklusos gráfok esetében (N - 1) nem zérus elemet fog tartalmazni,
ahol N a pontok számát jelöli, de ugyanazt az aciklusos gráfot (amelynek
neve a továbbiakban fa) NN-2 képen lehet beszámozni.
Bizonyítható, hogy amennyiben u.n. "fizikai" fát állítunk elő,
(ekkor minden sorszám olyan ponthoz kerül, amely szomszédos egy
már beszámozott ponttal) az alternatívák száma (N - 1)! A fizikai
fák az u.n. CAM kóddal írhatók le, amely lényegében egy sorvektor,
ennek i-edik eleme az A mátrix (i+1)
oszlopában az el nem tűnő elem sorszámát
adja meg. A variációk további csökkenése érhető el, ha a
beszámozására az u.n. Morgan algoritmust
alkalmazzuk. Ekkor a beszámozásnál arra is ügyelni kell, hogy a soronkövetkező
sorszám a legalacsonyabb sorszámú ponttal szomszédos még nem beszámozott
pont legyen. Az így jelölt fát "Morgan-fának" nevezzük. Bebizonyítottam,
hogy maximális - az az maximális CAM kódjelű, ha a kód számjegyeit
összevonjuk - Morgan-fa akkor állítható elő, ha az u.n LDF (lowest
degrees first) szabályt követjük a pontok beszámozása során.
Ekkor a Morgan szabályokon kívül arra is ügyelni kell, hogy az alacsonyabb
rendű (vegyértékű) pontokat kell előbb beszámozni. A fenti eljárással
képzett kódok egy primitív nyelv mondatai. E nyelv "nyelvta-nának"
- szintaktikus szabályainak - megválasztásával
elérhető, hogy a még redundáns szerkezetek, pusztán e szintaktikai
szabályokra való hivatkozás alapján felismerhetők és kiküszöbölhetők.
A fenti eljárás biztosítja szerkezeti izomerek nem-redundáns és egyben
teljes előállítását.
KVANTITATÍV
HATÁS-SZERKEZET ÖSSZEFÜGGÉSEK KORRÓZIÓS INHIBITOROK SORÁBAN
Lukovits István, Kálmán Erika
MTA, Kémiai Kutatóközpont
1525 Budapest, Pf.: 17.
Korróziós inhibitoroknak nevezzük azokat a vegyületeket
amelyek fémek vizes oldatokban végbemenő
korróziójának sebességét mérséklik. A ma alkalmazott korróziós
inhibitorok 1-10 mg/l koncentrációban már hatásosak. Vizsgálatainkat
semleges, vagy savas oldatokban ható molekulák sorában végeztük. Az
inhibíció hatékonyságát (E) az alábbi képlettel adtuk meg:
E = (vO - vi)/ vO ,
ahol vO jelöli a korróziós inhibitort
nem tartalmazó oldatban mért korróziós sebességet, és vi
jelöli korróziós inhibitort tartalmazó oldatban mért korróziós sebességet.
A korróziós sebesség értékét a legtöbb esetben az u.n. súlycsökkenés
módszerével határoztuk meg. vi és vO
értéke időben változik, ezért egyáltalán nem mindegy, hogy E értékét
milyen időintervallumban határoztuk meg. E értéke nem lehet 1-nél
nagyobb szám, de negatív szám lehet, ha a vegyület a korrózió sebességét
növeli, E egyben függ az alkalmazott inhibitor koncentrációjától
is. Vizsgálatainkban E és különböző
molekuláris paraméterek (megoszlási hányados, kvantumkémiai
indexek, molekula van der Waals felülete) között kerestünk összefüggéseket.
Mivel a kísérleti adatok az esetek döntő
többségében fix koncentrációjú oldatokra vonatkoznak, gondot jelentett
a koncentráció hatásának figyelembe
vétele. A levezetett lineáris regressziós egyenletek az inhibitorokat
adott koncentrációban tartalmazó oldatokra érvényesek, és nem biztos
hogy az ilyen egyenletekből levont következtetések érvényesek-e
más koncentrációjú oldatokra is. Ezért Langmuir (és egyéb) típusú
adszorpciót feltételezve nem-lineáris regressziós modellt fejlesztettünk
ki, amelyben a koncentráció hatását is figyelembe tudtuk venni. A nem-lineáris
regressziós módszerrel kapott egyenletek, mivel azok többféle koncentrációra
is érvényesek, statisztikai szempontból jóval felülmúlták a lineáris
regressziós módszerrel levezetett egyenletek szignifikanciáját. Ugyanakkor,
a kapott szoros illesztés jórészt a koncentráció változásnak, és
csak kisebb mértékben a molekuláris paraméterek megváltozásának
volt tulajdonítható.
ACETILÉN-SZÁRMAZÉKOK
KORRÓZIÓS INHIBÍCIÓS AKTIVITÁS-SZERKEZET ÖSSZEFÜGGÉSE
Kutsán György (*), Bundula
Róbert, Körtvélyesi Tamás, Rauscher Ádám
József Attila Tudományegyetem Fizikai Kémiai
Tanszéke
H-6721 Szeged, Rerrich Béla tér 1., Pf. 101
(*)Tel.: 62/450-000/4114 Fax: 62/311-943
(*)E-mail: kutsan@chem.u-szeged.hu
Acetilén-származékok (alkoholok,
aminok) inhibíciós hatékonyságát 1 M HCl-oldatban tervezett időtartamú
mérésekkel határoztuk meg. Méréseinkhez A38 minőségi
jelzésű hidegen hengerelt acélból készült próbatesteket használtunk.
A mintaelőkészítés standardizált műveletsorozattal történt. A tervezett
időtartamú méréseket a NACE Standard
TM-01-69 szabványnak megfelelően végeztük. A teljes kitéti idő 3
nap volt 30 °C-on, nitrogénnel oxigénmentesített oldatban. A mérési
eredmények alapján meghatározható a korróziósebesség valamint ennek
változásából az oldat korrozivitásának és a fém korrodálhatóságának
időbeni változása.
Az alkalmazott inhibítorok
néhány fizikai-kémiai jellemzőjét PM3 szemiempírikus kvantumkémiai
módszerrel számítottuk a SPARTAN 4.1 programrendszer felhasználásával.
A legstabilabb geometria fizikai-kémiai jellemzői - EHOMO
(Lowest Unoccupied Molecular Orbital), dipólusmomentum, nettó atomi töltések
és kötésrendek - és a korróziósebességek között lineáris regressziószámítással
kerestünk kapcsolatot. A kapott korrelációs együtthatók nem voltak
kielégítőek, ezért a legjobb korrelációt szolgáltató fizikai-kémiai
jellemzőkkel multilineáris regressziószámításokat végeztünk. Az
adatok vizsgálatát főkomponens analizissel (PCA) egészítettük ki.
A p <= 0.01 szignifikanciaszinten
korrelációt találtunk a korróziósebességek logaritmusa és a hármaskötés
kötésrendje, az ELUMO,
a dipólusmomentum értéke, az inhibítorok funkcióscsoportját hordozó
és a hármaskötés szénatom töltése között. A különböző kitéti
időkhöz tartozó korróziósebességekből levonható következtetések
(az oldat korrozivitásának és a fém korrodálhatóságának
változása) és a számított korrelációs együtthatók változásának
tendenciája arra utal, hogy a korróziós folyamat során az inhibítorok
olyan átalakuláson mennek keresztül az oldatban, amelynek révén többnyire
nagyobb inhibíciós hatékonyságú termékek képződnek.
FOLYADÉKKROMATOGRÁFIÁS
ELEMZÉSEK OPTIMÁLÁSA KISÉRLETTERVEZÉSSEL, SZIMPLEX MÓDSZERREL ÉS
CSÚCSALAKELEMZÉSSEL.
Pap Tamás - Pápai Zsuzsa
Veszprémi Egyetem, Analitikai Kémia Tanszék,
8201 Veszprém, Pf.:158.
Fenol-származékok intenzív folyadék-kromatográfiás
elválasztásánál a kromatogramok kiértékelését gyakran zavarják
átlapoló csúcsok. A kromatográfiás körülmények változtatásával
az egyes felbontási értékek általában javíthatóak, sok esetben azonban
más felbontási értékek romlani fognak. Kísérlettervezés [1, 2], szimplex
optimálás [3] és csúcsalakelemzés [4-6] segítségével az optimális
paraméterkombináció gyorsan meghatározható.
Kísérleteinket fenol-származékok
különböző összetételű keverékeivel végeztük az alábbi
kisérleti körülmények mellett:
Állófázis: LiChrosorb RP-18
Oszlop: 250 x 3.0 mm
Hőmérséklet: 25 °C
Detektor: UV 280 nm
Koncentráció: 2.5 x 10-2 mól/l
Az optimális paraméterkombináció
meghatározásához a kromatogramon előforduló két legkisebb felbontásértéket
választjuk ki és képezzük a hányadosukat oly módon, hogy mindig a
kisebb felbontást osztjuk a nagyobb értékkel
A kisérlettervezés során a paraméterek értékét
úgy változtatjuk, hogy a két legkisebb felbontás hányadosa minél
jobban megközelítse az 1,0 értéket (Ra /Rb, ahol Ra < Rb). Az első négy kisérlet során kapott adatokból meghatározzuk az
eredményfelület legmeredekebb emelkedésének irányát és a gradienskisérletek
során a paramétereket ebben az irányban változtatjuk az optimum
eléréséig.
Szimplex optimálás esetén
a kiindulási szimplex legrosszabb eredményét tükrözzük a szemközti
oldal középpontján és a tükrözött pontban leolvasható paraméterekkel
végezzük a következő kisérletet, majd meghatározzuk az új
szimplex legrosszabb eredményét és így haladunk
az optimális paraméterkombi-náció felé. Általában célszerű több
szimplex fejlesztését elindítani, mert az opti-málás folyamata gyakran
lokális optimumba fut be, vagy a szimplex két pontja az eredményfelület
gerincére lép fel, ami megakadályozza az optimális érték elérését.
A kromatográfiás csúcsok jellemzésére jól használhatók
a statisztikai momentumok is, melyek információt nyújtanak a csúcs
alakjára, szélességére, csúcsosságára és aszimmetriájára. Ezek
a faktorok felhasználhatók a csúcsok matematikai leírására szolgáló
egyenletek paramétereiként is.
1 Box,G.E.P. - Wilson,K.B.: J. Roy. Statist. Soc., B,
13 (1), 1-45 (1951).
2 Box,G.E.P.: Analyst, 77, 879-891 (1952).
3 Nelder,J.A. - Mead,R.: Computer J., 7, 308-313
(1965).
4 Grushka,E., Anal. Chem., 44, 1733 (1972)
5 Foley,J.P., Dorsey,J.G., Anal. Chem., 55, 730
(1983)
6 Yau,W.W., Anal. Chem., 49, 395 (1977)
ANALITIKAI MÓDSZEREK
VALIDÁLÁSA. MEGFELELÉS A CÉLNAK.
(The fitness for purpose of analytical method)
Hlavay József
Veszprémi Egyetem, Föld- és Környezettudományi Tanszék
Az analitikai kémiában
a kémiai információszerzés lehetőségei az alábbiakban foglalhatók
össze: milyen elemeket, vegyületeket, molekulákat, stb. tartalmaz a
minta: minőségi analízis, mennyi az alkotók relativ koncentrációja,
mekkora a várható koncentráció tartomány: mennyiségi analízis, milyen
az alkotók térbeli elhelyezkedése: a felületen és a minta teljes tömegében
lévő alkotók aránya, hogyan változik a minta összetétele az időben:
megfigyelési (monitoring) rendszerek kialakítása, milyen a mintát alkotó
elemek fizikai és/vagy kémiai formája: módosulat, molekulafajta
meghatározása (speciation).
A vizsgáló laboratóriumokban
a leggyakrabban az alkotók minőségi azonosítását és mennyiségi
meghatározását végzik el. Ha a vizsgálatok során az érvényben lévő
szabvány alkalmazható az alkotó
meghatározására, akkor az analitikus azt használja, ha nincs megfelelő
előírás, akkor módszert kell fejleszteni. Az analitikai mérésnek
megbizhatónak kell lenni és számos követelményt kell kielégíteni.
A kifejlesztett analitikai módszert validálni kell.
A EURACHEM által készített
Method Validation Guide [1] hat pontban foglalta össze azokat az analitikai
tulajdonságokat, amelyeket figyelembe kell venni a megbizó teljeskörű
kiszolgálásáért:
1. Az analitikai méréseknek
meg kell felelni az előzetes követelményeknek.
2. A mérések során olyan
módszereket és műszert kell használni, amelyekről előzetesen
meggyőződtünk, hogy a céloknak megfelelnek.
3. Az analitikusnak megfelelő
képesítéssel és tudással kell rendelkezni a feladat elvégzéséhez.
4. A labor tevékenységét
időközönként független szervezetnek meg kell vizsgálni.
5. Az egyik laboratóriumban
végzett mérésnek összevethetőnek kell lennie a másikban végzett
elemzésekkel.
6. Az analízist végző
szervezetnek jól definiált QA (Quality Assurance, minőségbiztosítás)
és QC (Quality Control, minőségellenőrzés) eljárásokkal kell rendelkeznie.
A feltételeknek csak jól felkészült analitikus és
laboratórium tud megfelelni. A "profi" analitikus tudja, hogy ha nem
megbizható az analízis, nincs értéke, felesleges a mérést elvégezni.
A megbízás bizalom, az analízisnek meg kell felelni a célnak. Annak
a célnak, amelyért az analízist elvégezték. Az analitikai mérések
eredményeinek megadásánál figyelembe kell venni a mérési bizonytalanságot.
A mérési eredményeken alapuló döntések hatékonysága jelentős
mértékben függ a mérési bizonytalanságtól.
Az analitikai módszer validálása olyan tevékenységek
összesége, amelyek a mükődési paraméterek
becslésére irányulnak és annak megerősítése, hogy a kidolgozott
analitikai módszer alkalmas egy egyedi feladat megoldására. A
módszer fejlesztés-validálás fontossága jelentős,
hiszen csak Magyarországon több millió mérést végeznek évente elsősorban
a klinikai vizsgálatok, a termékek
minőségellenőrzése, a környezeti minták analízise, kriminológia,
stb. területén. A mérések költsége nagy, a döntések kockázata
a megbizható analitikai mérésekkel csökkenthető.
1. EURACHEM Draft 2.0-5/97, The fittness for purpose of
analytical methods, May, 1997.
VÉGET
ÉRT A KEMOMETRIAI FORRADALOM?
Héberger
Károly
Magyar
Tudományos Akadémia, Kémiai Kutatóközpont, Kémiai Intézet
1025 Budapest II. K Pusztaszeri út 59/67; 1525 Budapest
Pf. 17.
tel: 325 79 00; fax: 325 75 54; email: heberger@cric.chemres.hu
Stephan D Brown indítja így rendezetlen gondolatait
a kemometriáról [1], melynek ismertetésére vállakoztam. A cikkből
kiderül milyen problémákat lát a szerző a kemometriával kapcsolatban.
Az elemzés történelmi ismertetővel kezdődik, hogyan alakult ki a kemometria,
milyen nézetek vannak erre vonatkozóan.
A kemometria definíciója sokféle lehet, kis túlzással
azt mondhatjuk, ahány kemometrikus annyi definíció. A szük meghatározás
statisztikai módszerek analitikai kémia területén történő alkalmazását
tekinti kemometriának. Van aki a többváltozós módszerek alkalmazásához
kapcsolja a fogalmat és vannak akik minden új tudományos ismeretet beleértenek
ami a kémia és a számítógépek összekapcsolásával állhat elő.
Talán a legelterjedtebb definíció a kísérlettervezést, az irányított
információszerzést is magában foglalja. Egyértelműen beletartozik
az optimalizálás, jelfeldolgozás, keverék felbontás (resolution of
mixtures, unmixing), többváltozós kalibrálás, paraméterbecslés,
szerkezet-hatás összefüggések keresése, mintázatfelismerés, mesterséges
intelligencia módszerei (szakértői rendszerek) és még a könyvtári
keresés is.
A vitaindítóból kiderül hogyan lehet a nehézségeket
legyőzni, hogyan kell (kellene) a kemometriát oktatni. Megvitatjuk az
un. százas szabály meglétét is. Választ kesresünk a kérdésre: alkalmazók
vagy fejlesztők-e a kemométerek? Ezenkívül a hazai tapasztalatokat
"kerekasztal-beszélgetés" jelleggel fogjuk megbeszélni.
Az utolsó két évben megjelent cikkekből leszűrhető
tendenciákat az Analytical Chemistry összefoglaló cikke alapján ismertetem
[2].
[1] Steven D. Brown, Has the "Chemometrics revolution"
Ended? Some Views on the Past, Present and Future of Chemometrics http://www.emsl.pnl.gov:2080/docs/incinc/chem_PHD.html
[2] B. K. Lavine, Chemometrics, Analytical Chemistry,
70, 209R-228R (1998).
SZENZOROK SZELEKTIVITÁSÁNAK
JELLEMZÉSE
Horvai György
BME Kémiai Informatika Tanszék
horvai@ch.bme.hu
A kémiai érzékelők (vagy akár teljes mérőrendszerek) szelektivitásának leírása nehezen
általánosítható, ha a válaszfelületek (mért jel az összes számbajövő
komponens koncentrációja függvényében) különböző tipusú függvények.
A szelektivitási adatokat azonban rendszerint csak kisebb mérési hibák
becslésére, korrigálására használják. Ezért érdemes a válaszfelületet
a mérni kívánt komponens válaszgörbéje közelében lineárisan közelíteni.
Így egy teljesen általános jellemzési módot kapunk.
A potenciometriás érzékelők
alkalmazásánál vannak olyan fontos esetek is, amikor az előbbinél
ponosabb leírásra van szükség. A válaszfelület évtizedek óta használt
empirikus egyenlete azonban helytelennek
bizonyult. Az új, pontosabb válaszfüggvény első levezetése bonyolult
volt és új, nehezen értelmezhető fogalmak bevezetésével járt. Sikerült
megmutatni, hogy a zavart az a fel nem ismert (de egyébként triviális)
jelenség okozta, hogy bár a modell paraméterek száma nagyobb volt az
egyenletek számánál, az egyenletrendszer mégis megoldható volt.