A kisérleti adatok jellemzése, ábrázolása és jelölése. Objektumok és tulajdonságok. Az adatmátrix, a tulajdonság- és objektumvektorok. Adatok ábrázolása lineáris térben és alterekben. Pontdiagrammok, felületek, elliptikus kontúrú térrészek. Adatok transzformálása, skálázása.

Nem felügyelt eljárás (más néven fürtelemzés) a teljes mintából kiindulva, a megfigyelt változók értékei alapján a minta egyedeit próbálja viszonylag homogén csoportokba rendezni. Az u.n. hierarchikus fürtelelmzés a csoportok közötti viszonyok feltérképzésére is vállalkozik, míg a nem-hierarchikus eljárások eltekintenek ettől. A fürtelemzés indulásánál tehát még nem rendelkezünk csoportokkal, az eljárás végére viszont csoportokhoz jutunk. A távolság-fogalom meghatározása, és megválásztásának jelentősege valamint változatai (eukleidészi, Machalanobis, Tanimoto stb). A kapcsolódási szabályok és a súlyozás fajtái és jelentőségük.

Felügyelt eljárás (más néven osztályozás) egy csoportosított minta egyedeire kiszámítja a különböző csoportokhoz való tartozás valószínűségeit, így az atott mintatérben megítélhetjük a csoportosítás jóságát. A diszkriminancia elemzés a megfigyeléseket a mintatérből egy olyan diszkrimináló térbe viszi át, ahol a csoportok a lehető legjobban elkülönülnek, és kiválasztjuk azokat a változókat, amelyek a csoportok különbözőségét határozottan magyarázzák. A szeparáló eljárások azokat a hiperfelületeket keresik, amelyek elválasztják egymástól a minta osztályait feltételezve, hogy az azonos osztályokban szereplő elemek “közel”, a különböző osztályokban szereplők pedig távol helyezkednek el egymástól. A csoportosítást alakfelismerésnek nevezik, ha a mintahalmaz elemeit képek, görbék alkotják.

Bevezetés, nevezéktani problémák. A főkomponens-elemzés lényege. A NIPALS algoritmus működése. A főkomponens-elemzés alkalmazása, példák. Faktoranalízis és rokon technikák. Ajanlott irodalom

A főkomponens-elemzés az adatok leegyszerűsítését teszi lehetővé, a kiindulási adatmátrix dimenziójának csökkentésével. A régi változók (oszlopok) lineáris kombinációjával új változókat állítunk elő a sajátérték probléma megoldásával. A főkomponenselemzés mögöttes gondolata az, hogy kisszámú háttérváltozó “underlying factor” segítségével a teljes mátrixot viszonylag jól (adott hibával) reprezentálni lehet. Az új változók korrelálatlanok (ortogonálisak), és csökkenő sajátérték sorrendjében szokás sorbarakni őket.

A főkomponens-elemzés sémaszerű ábrázolása:

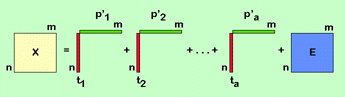
ahol X a kiindulási (elemzendő) adatmátrix, E a hiba (reziduum mátrix) mindkettő m sorból és n oszlopból áll, p_i (i=1, 2, a), a < m a főkomponens-súly (loading); t_j = (1, 2, a) a < n maga a főkomponens (főkomponens változó, score). Ha “a” megegyezik n-el illetve m-el akkor az utolsó főkomponensek tartalmazzák a hibát, és elhanyagoljuk ezeket.

Arra nincs egyértelmű szabály, hogy hány új főkomponens változót célszerű a modellben tartani. Többféle ajánlás is létezik, itt csak a hegyomlás-ábrát említem meg, melynek vizuális értékelésével lehet a változó számot meghatározni. Ezenkívül sokat segít a tapasztalat, az intuíció, a hibaszintek és az adott probléma ismerete. A főkomponenselemzés eredményeként kapott új változóknak (absztrakt faktoroknak) nem mindig lehet megtalálni a fizikai értelmét. Megjegyzendő, hogy a legteljesebb zűrzavar uralkodik a főkomponenselemzés, a faktoranalízis és rokon technikák nevezéktana körül. A legegyszerűbb kifejezéseknek (row designee, score stb.) sincs elfogadott magyar megfelelője, amelyeknek pedig van (pl. loading = súly illetve töltés), az félrevezető. Malinowski és Howery összefoglaló könyve [1] megadja, hogy 4 féle módon lehet a kiindulási mátrixot előkészíteni az elemzéshez. Elemezhetjük a kovariancia vagy a korrelációs mátrixot mindegyiket centrálással vagy anélkül. Ha az egyes mátrix elemek mérési hibája elhanyagolható az elemek egymáshoz képes vett változásához akkor a korrelációs mátrixot célszerűbb elemezni. A főkomponenselemzés részletes ismertetése megtalálható a [1,2]-ben, az elvét érthetővé teszi Christie munkája [3] alkalmazására példákat pedig [4-6]-ban.

Irodalom:

[1] (a) E. R. Malinowski, Factor Analysis in Chemistry, 2. kiadás, John Wiley and Sons, New York, 1991; (b) E. R. Malinowski és D. G.Howery, Factor Analysis in Chemistry, John Wiley and Sons, New York, 1980.

[2] S. Wold, K. Esbensen és P. Geladi, Chemometrics and Intelligent Laboratory Systems, 2, 37 (1987).

[3] O. H. J. Christie, Chemometrics and Intelligent Laboratory Systems, 2, 53 (1987).

[4] S. Vajda, P. Valkó és T. Turányi, Int. J. Chem. Kinet., 17, 55 (1985).

[5] K. Héberger, A. Németh, L. Cotarca, P. Delogu, Appl. Catal. A. General, 119, L7 (1194).

[6] K. Héberger és A. Lopata, J. Chem. Soc. Perkin Trans. 2, 91 (1995).

(A mérési hibák Gauss-eloszlásúak) Esetek: (a) Többváltozós lineáris regresszió, ha az X prediktív (független) változók hibája elhanyagolható, vagy zérus. Paraméterbecslés a legkisebb négyzetek módszerével, a maximális valószerűség (maximum likelihood) elvével, a momentumok módszerével, egyéb módszerekkel. (b) Többváltozós lineáris regresszió, ha az X prediktív változók hibája nem hanyagolható el (nem lehet különbséget tenni függő és független változó között!). Többváltozós normális eloszlás jellemzése, korrelációs koefficiens, parciális korrelációs koefficiens. (c) Több Y predikált (függő) változó.

A többváltozós lineáris regresszió érvényesítése (validálás) és diagnosztikája. Varianciaanalízis, többváltozós determinációs együttható, a reziduálisok vizsgálata, prediktív változók szignifikanciája. Többváltozós hibaanalízis, hibaterjedés. Paraméterek szignifikanciája, konfidencia intervallum. Keresztérvényesítés (cross validation): egyszerre egyet, egyszerre többet, adatok felét kiválasztva.

Többváltozós nemlineáris regresszió. Paraméterbecslés a legkisebb négyzetek módszerével, a maximális valószerűség (maximum likelihood) elvével, a momentumok módszerével, egyéb módszerekkel.

(A mérési hibák nem Gauss-eloszlásúak) Robusztus regressziós módszerek. Fuzzy elméleten alapuló regressziós módszerek. Paraméterek jellemzése bootstrap, jackknife és egyéb Monte-Carlo módszerekkel.

(A paraméterek sztochasztikus változók.) Bayes-becslés.

Többváltozós kalibráció. (a) Tenzoriális kalibráció. (b) Nulladrendű kalibráció: Egyváltozós legkisebb négyzetek módszere. Matrix hatás, standard addíció (SAM). (c) Elsőrendű kalibráció: Klasszikus modell, inverz modell. Közönséges többváltozós legkisebb négyzetek módszere (OLS). Pszeudoinverz: főkomponens regresszió (PCR), részleges legkisebb négyzetek (PLS) módszere. Bilineáris adatok. Matrix hatás, általánosított standard addíciós módszer (GSAM). (d) Másodrendű kalibráció: csatolt (kötőjeles) készülékek, pl. GC-MS. Általánosított rang-megsemmisülés módszere (generalized rank annihilation method, GRAM). Trilineáris adatok. (e) Harmad és magasabbrendű kalibráció: N-móduszú módszerek (N-way calibration). Multilineáris adatok.

Kalibráció hatékonyságát jellemző mennyiségek (figures of merit). Szabatosság: érzékenység, szelektivitás, pontosság (reprodukálhatóság és torzítatlanság), jel/zaj viszony. Reprezentativitás: mintavétel, mintaelőkészítés. Spektrális kölcsönhatások: háttér, eltolás, alapvonal.

Nemlineáris többváltozós kalibrációs módszerek: Helyileg súlyozott regresszió (LWR), leképezés keresés regresszió (projection pursuit regression), alternáló feltételes várakozás (ACE), többváltozós adaptív simító görbevonalak (MARS), mesterséges ideghálózatok (ANN), főkomponens regresszió (PCR), részleges legkisebb négyzetek (PLS) módszere.

A modellek paraméterbecslésénél fellépő problémák (kollinearitás, nem lineáris modellek, modellek teljes hiánya). A torzított regressziók jelentősége. Főkomponens regresszió, ridge regresszió. A predikciós feladatok kiterjesztése bonyolult esetekre: PLS, ideghálózatok, genetikus algoritmusok. Ajánlott irodalom.

Változó szelekció:

Tapasztalati összefüggések keresése közben mindig felmerül a leíró változók közti választás kényszere, egyrészt mivel minél kevesebb változóval kívánjuk leírni a jelenséget, másrészt mivel csak lényegi, valóban meghatározó változókat kívánunk szerepeltetni, a zajt lehetőség szerint el kívánjuk távolítani, hogy a leírás minél pontosabb, szabatosabb legyen. Ha a változók korreláltak (a változók, mint vektorok, egymás lineáris kombinációi) előfordul, hogy számos különbözőképpen kiválasztott változó csoport ugyanolyan szorosságú összefüggést eredményez. Az irodalomban számos megoldást találunk erre a problémára [1-7].

Jellemző a felsorolt cikkekben közölt eljárásokra, hogy a különböző algoritmusok ugyanazt a szelekciós kritériumot használják, és megfordítva egyazon algoritmuson belül különböző kritériumokat lehet felhasználni. Ezért is természetes, hogy e módszerek gyakran nem ugyanazt az eredményt szolgáltatják, mint a többi.

A változó kiválasztó módszereket többféleképpen is csoportosíthatjuk:

Nincs olyan matematikai statisztikai eljárás mely megmondaná, hogy melyik módszerrel kapott eredmény jobb, vagy rosszabb, ezért gyakoriak az olyan modellek melyek statisztikalilag megkülönböztethetetlenek. Egy adott problémára mindig alkothatunk több, egyenértékű modellt. Ez különösen a gyakorlatlan modellépítőt zavarja meg hiszen a statisztikailag egyenértékű, annak tűnő modellek más és más feltevésekkel készülnek, más elmélettel magyarázhatók, stb. Az egyes leíró változóknak más és más lehet a ”magyarázó” erejük. Egyikük-másikuk könnyen elméletbe illeszthető, mások a legujabb elméletek fényeben is értelmezhetetlenek (ami nem zárja ki azt, hogy később sikerül megfelelő elméletet találni). Ezen a problémán segíthet a párkorrelációs módszer (Pair-Correlation Method, PCM), amely statisztikailag egyenértékűnek tűnő változók között is tud választani, ha ez a különbség bizonyos szempontból létezik.

Irodalom

[1] (a) N.R. Draper and H.S. Smith, Applied Regression Analysis (Second Edition), John Wiley & Sons Inc., New York, 1981, Chapter 6, Selecting the “Best” Regression Equation, pp. 294-379. (b) M.L. Thompson, Selection of Variables in Multiple Regression: Part I. Review and Evaluation, International Statistical Review 46 (1978) 1-19 and (c) Part II. Chosen Procedures, Computations and Examples, Ibid 46 (1978) 129-146. (d) R.R Hocking, The Analysis and Selection of Variables in Linear Regression, Biometrics, 32 (1976) 1-49. (e) K.G. Kowalski, On the Predictive Performance of Biased Regression Methods and Multiple Linear Regression, Chemometrics and Intelligent Laboratory Systems, 9 (1990) 177-184.

[2] (a) G.P. McCabe, Principal Variables, Technometrics, 26 (1984) 137-144. (b) W.J. Krzanowski, Selection of Variables to Preserve Multivariate Data Structure using Principal Components, Applied Statistics, 36 (1987) 22-33. (c) I.T. Jolliffe, Discarding Variables in a Principal Component Analysis. I: Artificial Data, (d) I.T. Jolliffe, Discarding Variables in a Principal Component Analysis. II: Real Data, Applied statistics,

[3] (a) F. Lindgren, P. Geladi, S. Ränner and S. Wold, Interactive Variable Selection (IVS) for PLS. Part I. Theory and Algorithms, Journal of Chemometrics, 8 (1994) 349-363. (b) F. Lindgren, P. Geladi, A. Berglund, M. Sjöstrom and S. Wold, Interactive Variable Selection (IVS) for PLS. Part II. Chemical Applications, Journal of Chemometrics, 9 (1995) 331-342. (c) N.J. Messick, J.H. Kalivas and P.M. Lang, Selecting Factors for Partial Least Squares, Microchemical Journal, 55 (1997) 200-207. (d) U. Norinder, Single and Domain Mode Variable Selection in 3D QSAR Applications, Journal of Chemometrics, 10 (1996), 95-105.

[4] (a) J.H. Wikel and E.R. Dow, The Use of Neural Networks for Variable Selection in QSAR, Bioorganic & Medicinal Chemistry Letters, 3 (1993) 645-651 and (b) J.H. Wikel*, E. R. Dow, and M. Heathman, Interpretative Neural Networks for QSAR, http://www.awod.com/netsci/Issues/March96/feature1.html. (c) V. V. Kovalishyn, I.V. Tetko, A.I.Luik, V.V. Kholodovych, A.E.P. Villa and D.J: Livingstone, Neural Network Studies. 3. Variable Selection in the Cascade-Correlation Learning Architecture, 38 (1998) 651-659. (d) F. Despagne, D-L. Massart, Variable Selection for Neural Networks in Multivarate Calibration, Chemometrics and Intelligent Laboratory Systems, 40 (1998) 145-163).

[5] (a) H. Kubinyi, Variable Selection in QSAR Studies. Part I. An Evolutionary Algorithm Quantitative Structure Activity Relationships, 13 (1994) 285-294 and (b) Part II. A Highly Efficient Combination of Systematic Search and Evolution, ibid 13 (1994) 393-401. (c) D. Jouan-Rimbaud, D.-L. Massart, R. Leardi, O.E.de Noord, Genetic Algorithms as a Tool for Wavelength Selection in Multivariate Calibration, Anal. Chem., 67 (1995) 4295-4301, (d) H. Kubinyi, Evolutionary Variable Selection in Regression and PLS Analyses, Journal of Chemometrics, 10 (1996), 119-133. (e) R. Leardi, A.L. Gonzáles, Genetic Algorithms Applied to Feature Selection in PLS Regression: How and When to Use Them, Chemometrics and Intelligent Laboratory Systems, 41 (1998) 195-207. (f) A.S. Bangalore, R.E. Shaffer, G.W. Small and M.A. Arnold, Genetic Algorithm-Based Method for Selecting Wavelength and Model Size for Use with Partial Least-Squares Regression: Application to Near-Infrared Spectroscopy, Anal. Chem., 68 (1996), 4200-4212.

[6] (a) J.M. Sutter and J.H. Kalivas, Comparison of Forward Selection, Backward Elimination, and Generalized Simulated Annealing for Variable Selection, Microchemical Journal, 47 (1993) 60-66. (b) J.M. Sutter, S.L. Dixon and P.C. Jurs, Automated Descriptor Selection for Quantitative Structure - Activity Relationships using Generalized Simulated Annealing, Journal of Chemical Information and Computer Sciences, 35 (1995) 77-84. (c) J.H. Kalivas, N. Roberts and J.M. Sutter, Global Optimization by Simulated Annealing with Wavelength Selection for Ultraviolet-Visible Spectrophotometry, Analytical Chemistry, 61 (1989)2024-2030.

[7] (a) V. Centner, D-L. Massart, O.E. de Noord, S. de Jong, B.M. Vandegeniste and C. Sterna, Anal. Chem., 68 (1996), 3851-3858. (b) B.K. Alsberg, A.M.Woodward, M.K. Winson, J.J. Rowland, D.B. Kell, Variable Selection in Wavelet Regression Models, Analytica Chimica Acta, 368 (1998) 29-44.

Bevezetés. A főkomponens-regresszió lényege. A főkomponens-regresszió alkalmazása, többváltozós kalibráció. Ajánlott irodalom

A főkomponens-regresszió (principal component regression, PCR) fölfogható úgy is, hogy a leíró változók (deszkriptorok) főkomponens-elemzése után az új változókat tekintjuk független változóknak és többváltozós regressziót végzünk a függő változó és közöttük. Azaz klasszikus változó szelektálási problémáról van szó. A régi változók (X vektorok) lineáris kombinációjával új változókat állítunk elő melyek korrelálatlanok (ortogonálisak) lesznek, és közülük keressük meg azokat amelyek korrelálnak a függő változóval, az y vektorral. Ezáltal olyan előrebecslést kapunk a függő változó értékére mely használja ugyan az összes leíró változóban meglévő információt, de a hibának csak egy részét, rendszerint a kisebb részét. Így az előrebecslés hibája kisebb lesz mintha az eredeti változókat használnánk, de csak annak az árán, hogy szisztematikus hiba kerül a becslésbe.

A kemometria kézikönyve [1] a főkomponens-regressziónak két előnyét emeli ki a többváltozós regresszióval szemben: (1) Alig néhány változóra van szükség. Példájukban 1050 eredeti változó helyett 14 főkomponens is elegendő. Ez az előny azonban látszólagos, mert a 14 új változó előállításáshoz mind az 1050 régire szükség van. (2) A változók korrelálatlansága oda vezet. hogy az előrebecslés minősége megjavul, azaz hibája csökken.

Kalibrációs módszerként fölfogva a PCR-t a lineáris inverz model megoldására használhatjuk [2]:

c = Rb + e

ahol R a készülék válaszjel mátrixa egy sor kalibrációs mintára vonatkozóan (pl. spektrumok), c az összes minta koncentrációja (vektor), b a modell paramétereit tartalmazó vektor és e a koncentrációk reziduumának vektora. A PCR becsli a b regressziós vektort a pszeudo-inverz kiszámításával, ilyeténképpen:

b’ = R⁺ c

A pszeudo-inverzet egy háromlépéses eljárással határozhatjuk meg. Először a válaszjel mátrixot három mátrixra bontjuk:

R⁺ = USV^T

ahol U és V oszlopai ortonormáltak és S diagonális.

Ezután egy kisebb dimenziójú közelítést végzünk, úgy hogy a lényegi információt megtartjuk a zajt pedig kiszűrjük. Végül ennek a közelítésnek a pszeudo-inverzét számítjuk ki:

R⁺ = U S^–1 V^T

ahol az aláhúzások azt jelzik, hogy a mátrixokat az optimális pszeudo-rangúra csökkentettük.

A pszeudo-rang meghatározása fontos és kritikus, mert a modellnek le kell irnia az összes fontos variancia forrást, de nem szabad túlilleszteni az adatokat.

A PCR-t gyakran összehasonlítják a parciális legkisebb négyzetek (partial least squares, PLS) módszerével. Általában a PLS jobb eredményeket ad (kisebb hibát és jobb értelmezhetőséget is) de ez nem szükségszerű [3]. A jobb eredmények oka, hogy a függő változóban (y) meglévő információt is fölhasználjuk a becslés során. Viszont könnyen találhatunk olyan példákat ahol a PCR felülmúlja a PLS-t, ám rendszerint a különbség nem jelentős. Ha a függő változó (y) nagyon pontatlan a PLS komponensek sem lesznek értelmezhetőek.

Irodalom:

[1] D. L. Massart, B. G. M. Vandeginste, L. M. C. Buydens, S. De Yong, P. J. Levi, and J. Smeyers-Verbeke, Handbook of Chemometrics and Qualimetrics: Part A, Elsevier, Amsterdam, 1997.

[2] S. Sekulic, M. B. Seasholtz, Z. Wang, B. R. Kowalski, S. E. Lee and B. R. Holt, Analytical Chemistry, 65, 835A (1993)

[3] R. G. Brereton, Chemometrics Application of Mathemetics and statistics to laboratory Systems, Ellis Horwood, New York, 1990.

Sztochasztikus (sztch.) változók, sztch. folyamatok meghatározása. A sztch. folyamatok felosztása:

folytonos, nem folytonos (diszkrét), független és nem független sztch. folyamatok (= idősorok ).

Markov láncok, a rendszer állapotai, kezdeti eloszlása, átmeneti valószínűségek, 1,2...r - lépéses szt. átmenetvalószínűség mátrixok, abszolút valószínűségek. Periodikus és nem periódikus Markov láncok, határeloszlástételek. Ábrázolás fadiagrammok segítségével. Példák különböző Markov láncokra.

Sztochasztikus összefüggések két valószínűségi változója közötti öszefüggés kifejezése a korrelációs együtthatóval, a függetlenség kifejezése a kovarianciával. Az autokovariancia és a keresztkoreláció fogalma.

Ábrázolás: szóródási diagrammok 4 esete: 1. nincs korreláció, 2. nincs korreláció ,de erős a függés, 3. lineáris függés, 4. általános szóródási diagramm. A korrelációs együttható számítása normális és nem-normális eloszlás esetében (nem-paraméteres rangkorrelációk: Spearman és Kendall szerint).

Példa: környezeti adatok közötti összefüggések vizsgálata (auto- és keresztkorrelációk)

Markov-folyamatok: definició, különböző Markov folyamatok (megszámolható sok állapottal, folytonos állapotváltozással, folytonos és ugrásszerű állapotváltozással). Példák Markov folyamatokra.

Sztch., nem Markov folyamatok, idő-vagy más valós paraméterű folyamatok. Rekurrens folyamatok. A véletlen folyamat teljes meghatározásának feltétele: a tetszés szerinti számú változó együttes eloszlásának megadása. Egy-két-n-dimenziós sürüségfüggvények. Sztch. függvények átlagolása: statisztikai és idő-átlagok, momentumok (szórások).

Stacionárius sztch. folyamatok, szigorúan stacionárius, k-ad rendben stac. folyamatok. Az ergodicitás fogalma és feltétele.

Korrelációs függvény: a sztch. folyamatpárok közötti kapcsolat kifejezése. Autokovariancia: a folyamat két mintavételi változója közöti kapcsolat kifejezése. Stacionárius másodrendű folyamat teljesítmény-spektrumának értelmezése a folyamat autokorrelációfüggvényének Fourier transzformáltjaként.

Példák sztch., nem-Markov folyamatokra: adott sürüségfüggvény mellett a valószínűségi változó értéke becsülendő adott t + t időpontban; adott korrelációs függvényből meghatározandó a spektrális sürüségfüggvény, Geiger-Müller számláló által t idő alatt regisztrált részecskék eloszlása, az eloszlás aszimptotikus kifejezése. Regisztráló készülékekkel kapcsolatos követelmények meghatározása (regisztrálás gyakorisága, kapacitás-problémák).

A `80-as évek közepéig reménytelennek látszott az olyan bonyolult, sokváltozós folyamatok matematikai modellezése melyek elméleti háttere nem tisztázott, de velük kapcsolatban jelentős tapasztalati tudás ill. elegendő számú mérési adat halmozódott fel, valamint a független és függő változók között nem lineáris összefüggés(ek) áll(nak) fenn. A tudományos köztudatba 1986-ban robbant be, a már a '70-es évek végén felfedezett, mesterséges ideg(sejt)hálózatok (Artificial Neural Networks) nevű nem lineáris közelítő eljárás.

Az emberi agy tanulási folyamatait, információfeldolgozását mesterséges ideghálózatokkal kísérelték meg utánozni. Miután az idegsejtekről szerzett ismereteink még ma is töredékesek, ráadásul a számítógépek teljesítőképességének is vannak határai, a fenti modellek szükségszerűen csak egyszerüsített másai a valódi ideghálózatoknak. Mint annyiszor a tudomány története során ismét kiderült, hogy a mesterséges ideghálózatok az agyműködést ugyan nem képesek tökéletesen utánozni, viszont az eddig matematikailag kezelhetetlen tudományos, műszaki problémák leírására kiválóan megfelelnek. Így mára az egyik legszéleskörűbben használt nem lineáris közelítő eljárássá váltak.

A mesterséges ideghálózatok egymással összekapcsolt modell-idegsejtekből épülnek fel. A kapcsolódási helyek, u.n. szinapszisok, működését egy módosítható hatékonysági tényező, a súly, fejezi ki. A legtöbb mesterséges idegsejthálózat nem követi a valódi idegsejtek dendritjeinek és axonjainak bonyolult térbeli elrendeződését. Az idegsejtek kimenő elektromos jelét egyetlen szám fejezi ki, amely az idegsejt aktivitásának mértékét jelöli. Mindegyik modell-egység egyetlen kimenő jellé alakítja át a beérkező impulzusok összességét, és azt továbbítja a többi egység felé. Az átalakítás két lépésben megy végbe. Elsőként minden beérkező jel a hozzá tartozó szinapszis hatékonysága szerinti súlyozó tényezővel szorzódik, majd a súlyozott értékek összeadásával kialakul az eredő bemeneti érték (input). A második lépésben a feldolgozó egység a megfelelő átalakító függvény szerint kiszámítja kimeneti jel (output) értékét. Ezekből a modell-idegsejtekből azután tetszőleges elrendeződésű hálózat építhető fel.

Egy mesterséges ideghálózat viselkedése a benne foglalt egységek kapcsolódási módjától, a súlytényezőktől, az átalakító (input-output) függvényektől függ. Ez utóbbi lineáris, lépcsős, szigmoid, sinus vagy arcus tangens tipusú lehet. A valódi idegsejtek leginkább a szigmoid tipusú függvényekre emlékeztetnek, és érdekes módón az adatmodellezésben is ez a típus bizonyult. Hogy a mesterséges ideghálózat el tudjon látni valamilyen meghatározott feladatot, meg kell választanunk az egységek kapcsolódási módját, és minden egyes kapcsolathoz hozzá kell rendelnünk a hatékonyságának megfelelő súlytényezőt. Az előbbi határozza meg, hogy valamely egység befolyást gyakorolhat-e egy másik egységre, az utóbbi értéke pedig a befolyás erősségét szabja meg.

A mesterséges idegsejtekből tetszőleges elrendezésű hálózat építhető fel. A leggyakrabban használt mesterséges ideghálózatok három vagy négy rétegből állnak: a bemeneti egységek rétege a közbülső egységek rétegével van összeköttetésben, amelyhez pedig a kimeneti egységek rétege csatlakozik. Kimutatható, hogy e három rétegű elrendezés szigmoid átviteli függvényt használva tetszőleges pontossággal közelíthet bármilyen lineáris avagy nem lineáris függvényt. Négyrétegű (bemeneti, két rejtett, kimeneti) hálózatok használata vélhetően nem deriválható vagy szakadásos függvények közelítésére célszerű. A közbülső csomópontok számának meghatározása elméletileg még nem tisztázott.

Régóta ismert, milyen N-dimenziós térben megtalálni azt az N paraméterértéket tartalmazó vektort, melyhez valamilyen szempontból optimális célfüggvény érték tartozik. Különösen, ha a célfüggvény nem monoton, hanem helyi szélsőértékeket is tartalmaz. A hagyományos sokváltozós szélsőérték kereső eljárásoknak (konjugált gradiens, Newton, simplex stb.) ez utóbbi esetben az optimum megtalálása csak véletlenül sikerül. Ezért fejlesztették ki a számításigényesebb globális szélsőérték kereső algoritmusokat

Szimulált megeresztés

A megeresztés régen ismert és alkalmazott fémmegmunkálási módszer, melynek során valamely szilárd anyagot az olvadáspontja fölé melegítenek majd lassan lehűtenek. A lassú hűtés lehetővé teszi, hogy az anyag atomjai a termodinamikailag legstabilabb, legalacsonyabb energiájú kristályszerkezetbe, u.n. egykristályba rendeződjenek. Viszont, ha az anyagot hirtelen hűtjük le nagyobb energiájú polikristályos vagy amorf szerkezetet kapunk (v.ö. fémek edzése). A statisztikus termodinamkai megközelítés szerint a termikus egyensúlyi állapotban levő rendszer elemeinek energiaeloszlása a Boltzmann valószínűségi eloszlást követi:

P(E) ~ exp(-E/kT)

ahol E az elemek energiáját, k a Boltzmann-állandót, T az abszolút hőmérsékelet jelenti. A fenti eloszlásból az is következik, hogy még kis hőmérsékleten is van valamekkora, bár igen kicsiny, esély arra, hogy a rendszer nagy energiájú állapotba kerüljön. Vagyis előfordulhat, hogy a rendszer kikerül a helyi minimumból és egy magasabb energiállapoton keresztül esetleg globális minimumba juthat. Leegyszerűsítve arról van szó, hogy a megeresztés során az atomok helyzetétól függó energiafüggvényt kell minimalizálni az atomok elmozdításával. Az eljárás, mivel bizonyosan sokdimenziós (3 * az atomok száma) és az energiafüggvény általában több helyi minimummal is rendelkezik (különböző energiájú kristályszerkezetek), sokdimenziós optimalizáló algoritmus kidolgozására ihlette Metropolist és munkatársait (köztük Teller Edét). Az általuk kifejlesztett szimulált megeresztés a szimplex továbbfejlesztésének is felfogható, csak a rendszer nem simán és gyorsan mászik lefelé a válaszfelületen, hanem lassan ugrálva. (A gyors konvergenciájú optimalizációs algoritmusokat viszont akár szimulált edzésnek is hivhatnánk).

Genetikus algoritmus

Ezen eljárás kitalálói így okoskodtak: legyen a paramétervektor n szám sorozata. A vektor korodinátái (pl. 10001110011000) "bitszalagot" képeznek. Olyan ez, mint egy kromoszóma. Egy-egy bit egy-egy adott lókuszon elhelyezkedő gén. Allítsunk elő véletlenszerűen több mesterséges kromoszómát. Ezek alkotják a "populációt". A populáció mérete legyen olyan nagy, hogy a vektorok egyenletesen szóródjanak szét az N-dimenziós paramétertérben Ezzel is kedvezünk a globális optimum megtalálásának. A mesterséges evolúcióban a vektor koordinátái nem csak 1 és 0, hanem bármilyen szám lehetnek.

Számítsuk ki most minden kromoszómához a hozzátartozó célfüggvényértéket. Eszerint lesznek jó vektorok és lesznek roszabbak Készítsünk most egy "párosodási listát", amelyre felveszük a kromoszómákat, a paramétervektorokat. Ha jók, többször is felkerülhetnek a listára, és leszorítják róla a gyengébbeket. Definiáljunk párosodási valószinűségeket és induljon el a kromoszómák között adott stratégia szerinti paraméterkicserélődés. A csere lezajlása után új generáció keletkezett. Döntés kérdése, hogy minden újszülött paramétervektor a szüleit pótolja-e, vagy a jó szülők és jó gyermekek keveréke legyen az új generáció. Várható - de nem minden esetben szavatolt - hogy minden generáció jobb célfüggvényértékű vektorokból áll. Hogy a lokális minimumokba való időelőtti beleszédülést megelőzzük, hogy a változatosságot fenntartsuk, engedjük adott valószínűséggel a paramétervektorokat mutálni is: generációnként és populációnként cseréljünk ki egy két bitet a kromoszómákban. A generációk keletkezése, azaz az optimális célfüggvényérték megközelítése akkor ér véget, ha születik olyan paramétervektor, amely a szélsőértéket előre az meghatározott leállási feltételnek megfelelően megközelítette.