A PÁRKORRELÁCIÓS MÓDSZERHEZ HASZNÁLT TESZTEK
ELSŐ ÉS MÁSODFAJÚ HIBÁINAK ELMÉLETI VIZSGÁLATA

Rajkó Róbert1, Héberger Károly2

1JATE Élelmiszeripari Főiskolai Kar, 6701 Szeged, Pf. 433.
E-mail: rajko@sol.cc.u-szeged.hu

2MTA Kémiai Kutatóközpont, Kémiai Intézet, H-1525 Budapest, Pf. 17.

Fax No: +36 1 325 75 54; telefon: +36 1 327 79 00

E-mail: heberger@cric.chemres.hu

 

A párkorrelációs módszer (Pair-Correlation Method, PCM) nemparaméteres változószelekcióra alkalmas eljárás. Előző vizsgálataink szerint [1-7] nagyon gyakran még akkor is alkalmazható, ha más paraméteres eljárás nem tud különbséget tenni a változók között. Bevezetéséhez mindenféleképpen értelmeznünk kell a korreláció fogalmát. Korreláció "általában két mennyiség értékének olyan függése egymástól, amelynek valószínűségi jellege van, vagyis az egyik mennyiség meghatározott értéke befolyásolja a másik lehetséges értékeinek sorozatát" [8]. A korreláció mértékének számszerű kifejezése lehet a korrelációs koefficiens (r), vagy ennek négyzete a determinációs együttható:

,

ahol M[.] a várható értéket, D[.] a szórást jelenti. A korrelációs koefficiens tehát csak akkor számítható, ha a benne szereplő véletlen változónak létezik a várható értéke és a szórása! Legelterjedtebben (persze gyakran mindenfajta ellenőrzés és igazolás nélkül) használt eloszlás a normális vagy Gauss-eloszlás, esetében a korrelációs együttható becsülhető. Nem ez a helyzet Cauchy-eloszlású véletlen változóknál, hiszen ennek sem várható értéke, sem szórása nem létezik (a megfelelő integrálok végtelent adnak). Cauchy-eloszlású két normális eloszlású véletlen szám hányadosa, tehát a kémiai praktikumban lépten-nyomon találkozhatunk vele, pl. az egyszerű százalékszámításnál, ha a viszonyított és a viszonyítandó értékek is normális eloszlásúak voltak.

Tehát sok más mellet a korrelációs együttható sem általánosan használható, ezért van szükség a korreláció más, eloszlástól független meghatározására. A PCM fejlesztésével egy ilyen eljárást szeretnénk bevezetni. A PCM használatához teszt-statisztikák alkalmazására van szükség. Eddig a következő próbastatisztikákat mutattuk be [4]:

A fejlesztett programban [3] mostanáig csak az első fajú hiba bekövetkeztét szabályozó valószínűség értéket () lehetett beállítani, de szükséges a másodfajú hiba bekövetkeztének valószínűségét () is ismernünk, hiszen a null-hipotézis H0 elutasítása, azaz a HA hipotézis elfogadása révén tudjuk azt állítani, hogy két változó közül melyik korrelál jobban a harmadikkal. A Fisher-féle egzakt tesztre bemutattuk az erőfüggvényt [7], melyet a HA : kB = k3 alternatív hipotézis felállításával nyertünk.

A HA valószínűsége:

,

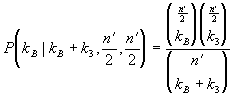ahol n' = kA + kB + k3 + kD. A másodfajú hiba valószínűsége

,

ebből a próba erőfüggvénye

.

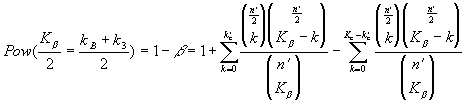Ez a levezetés azon alapult, hogy az alternatív hipotézis egyszerű hipotézis, ha összetett, akkor a levezetés is bonyolultabb lesz. Sajnos a bevezető matematikai statisztikai könyvek a másodfajú hiba, ill. az erőfüggvény tárgyalását a legegyszerűbb u-próba esetére részletezik csak, a többi próbánál gyakran már meg sem említik. Üdítő kivétel ez alól Kemény és Deák [9] legújabb könyve, mely a varianciaanalízis kapcsán tárgyalja a másodfajú hibát. Sajnos esetünkben ez az ismeret is kevésnek bizonyult, így először a kemometriai irodalomban bemutatjuk a PCM-hez használt próbastatisztikák másodfajú hibáinak számítását a matemataikai szakirodalomra támaszkodva, az ott megjelent információk nem kis erőfeszítést igénylő értelmezése alapján.

A kapcsolódó kutatásokat az AKP 98-51 2,4/19 illetve az OTKA F-025287 (R.R.), pályázatai támogatták.

IRODALOM

  1. R. Rajkó, K. Héberger: Algorithmic and statistical problems during development of a nonparametric variable selection method. CHEMOMETRICS V, Brno, Czech Republic, August 29 - September 2, 1999
  2. K. Héberger, R. Rajkó: Pair-Correlation Method with parametric and non-parametric test-statistics for variable selection. Description of computer program and application for environmental data case studies. Proceedings of 2nd International Conference on Environmental Engineering, Veszprém, 29th May - 5th June, 1999, pp. 82-91.
  3. Rajkó Róbert: Regressziós módszerek alkalmazása és fejlesztése a kémiai és élelmiszeripari mérések kiértékelése során. PhD Értekezés, BME, Budapest, 1998.
  4. Rajkó Róbert, Héberger Károly: A párkorrelációs módszer MS Excel VBA változata új teszt statisztikákkal. [MS Excel VBA version of the pair-correlation method with new test statistics] KEMOMETRIA '98, Miskolc-Lillafüred, 1998. október 7-9.
    Abstract: http://www.staff.u-szeged.hu/~rajko/prgabs.html#PCM VBA
  5. K. Héberger and R. Rajkó: Discrimination of statistically equivalent variables in quantitative structure-activity relationships. In Quantitative Structure-Activity Relationships (QSAR) in Environmental Sciences-VII, Ed. Fei Chen & Gerrit Schüürmann, SETAC Press, 1997, Ch. 29, 423-431
  6. R. Rajkó, K. Hébereger: Comparison of several test statistics for pair-correlation method. CC'97 Conferentia Chemometrica '97, 1th International Chemometric Conference in Hungary, Budapest, August 21-23, 1997, Abstract: http://www.staff.u-szeged.hu/~rajko/Pos52.gif
  7. Héberger Károly, Rajkó Róbert: Változókiválasztásra szolgáló pár-korrelációs módszer kiterjesztése több váltózóra kvantitatív szerkezet-hatás összefüggések keresésekor. KEMOMETRIA '95, Veszprém, 1995. október 18-20.
  8. Fizikai Kislexikon. (szerk. Szilágyi Miklós) Műszaki Könyvkiadó, Budapest, 1977.
  9. Kemény S. és Deák A. (1998): Kísérletek tervezése és értékelése. Műegyetem Kiadó, Budapest.