Ringler András

Mi köze van a szabályos háromszögnek a szabályos ötszöghöz?

Dolgozatomban azt mutatom meg, hogy kiindulva egy szabályos háromszögből, olyan adatokhoz juthatunk, amelyek segítségével egy szabályos ötszög körzővel és vonalzóval könnyedén megszerkeszthető.

A derékszögű háromszögekkel kapcsolatosan gyakran használt magasság-tételt szinte mindenki ismeri. Azt azonban már kevesebben tudják, hogy ez a tétel egy általánosabb tételnek, a szelőszakaszok-tételének csupán egy speciális esete. Könnyű megmutatni, hogy ezen állítások hátterében a kör tulajdonsága, "a kör egyenlete áll".

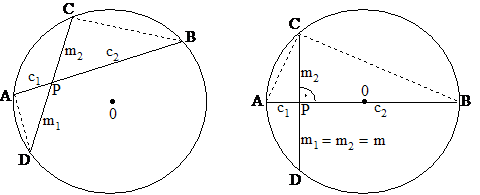
1. ábra. A kör két tetszőleges húrja a P pontban metszik egymást. A jobb oldalon speciális eset: az egyik húr a kör átmérője, a másik húr (a CD húr) pedig merőleges az AB átmérőre

Egy körben két egymást metsző AB és CD szelőszakasz (két húr) közös pontja legyen P. Az 1. ábra bal oldali részét nézve könnyű belátni, hogy az ADP D hasonló a PBC D-höz, Þ , Þ ; és ez minden, a P ponton átmenő szelőszakaszra igaz. Ha az AB szelőszakasz (speciális esetként) átmegy a kör középpontján (vagyis, ha az AB húr éppen átmérő, lásd az 1. ábra jobb oldali részét) és a CD szelőszakasz merőleges az AB szelőszakaszra, akkor az ABC háromszög derékszögű háromszög lesz, ekkor miatt . Ez utóbbi éppen a magasság-tétel, amely szerint a derékszögű háromszög átfogójához tartozó m magasság mértani közepe az átfogó megfelelő két részének.

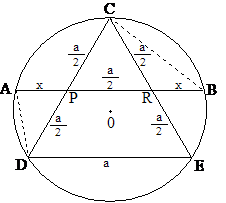
2. ábra. A szabályos háromszöget szemléltető ábra érdekessége, hogy az x és az távolságok (vagy a 2x és az a távolságok) aranyarányban vannak egymással. Aranyszomszédok ismeretében a szabályos ötszög, például a pitagóreusok titkos szimbóluma, a szabályos ötágú csillag könnyedén megszerkeszthető (lásd a 4. ábra jobb oldali részét!)

A szelőszakaszok-tételének ismerete hasznos dolog, segítségével válaszolhatunk a címben feltett kérdésre: mi köze van a szabályos háromszögnek a szabályos ötszöghöz? A kérdés megválaszolásához egy körbe rajzolt egyenlő oldalú DEC háromszög CD és CE oldalainak P és R felezőpontjaira húzott középvonal körrel közös pontjait jelölje A és B (lásd a 2. ábrát!). Az AB és CD húrok megfelelő (AP = RB = x, PB = , CP = PD = ) részeivel írjuk fel az előbb bevezetett szelőszakaszok tételét, így

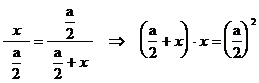. Ez az összefüggés azt mondja, hogy az távolság mértani közepe az és az x távolságoknak, amelyből az hiperbolikus egyenlethez jutunk. Mai ismeretekkel könnyű rájönni arra, hogy ezen egyenlet algebrai megoldásával és adódik. Ez a tény roppant érdekes, hiszen arról tájékoztat, hogy az x és az távolságok (vagy a 2x és az a távolságok) aranyarányban vannak egymással; az ilyen tulajdonságú távolságokat aranyszomszédoknak nevezem. Tudjuk, hogy a szabályos ötszög körzővel és vonalzóval történő megszerkesztéséhez aranyszomszédokra van szükség, ezek segítségével ugyanis a 72^o-os szög, a szabályos ötszög középponti szöge megszerkeszthető. A görögök idején az alakú (hiperbolikus) egyenleteket még nem algebrailag, hanem geometriailag, tehát körzővel és vonalzóval oldották meg; de mivel a görögök a negatív számokat nem ismerték, ezért a negatív megoldás nem is érdekelhette őket. A görögök által használt, a mára már elfelejtett geometriai módszer nagyon érdekes, felidézésével, pontosabban az újra történő felfedezésével - a megoldó képlet használata, tehát algebrai ismeretek nélkül - mutatom meg, hogy hogyan jöhetünk rá, hogy mi köze a fenti szabályos háromszögnek a szabályos ötszöghöz: a 2. ábrán olyan adatok vannak, amelyek segítségével szabályos ötszöget, például szabályos ötágú csillagot tudunk szerkeszteni. A 2. ábra másik érdekessége, hogy az AB húr hossza megegyezik a 3. ábrán látható derékszögű háromszög átfogójának a hosszával (ennek jelentőségét lásd később!).

Az alakban adott hiperbolikus egyenlet geometriai megoldhatósága felismeréséhez, egy "elfelejtett módszer" felidézéséhez, illetve az újból történő felfedezéséhez szorozzuk meg az alakú hiperbolikus egyenletet 4-gyel; Þ , Þ , Þ , Þ , Þ . Ez a kifejezés roppant érdekes, ez nem más, mint egy derékszögű háromszögre felírt Pythagorasz-tétel (lásd a 3. ábrát!). Az a és az távolságok, mint befogók ismeretében megszerkesztett derékszögű háromszög hosszúságú átfogója tartalmazza a keresett x távolság kétszeresét, a 2x-et; amelynek megfelezésével előáll a keresett x távolság. A szerkesztésből látszik, hogy az alakú egyenlet megoldhatóságának, a derékszögű háromszög megszerkeszthetőségének nincsen semmilyen geometriai akadálya (a 3. ábrán látható derékszögű háromszög minden a távolság esetén megszerkeszthető); az ilyen alakú egyenletek algebrai megoldásánál a diszkrimináns értéke mindig pozitív, tehát két gyököt, egy pozitív és egy negatív gyököt várunk (bár a negatív gyököt szigorú görög mestereink nem találták meg, hiszen nem is keresték). Ha a távolságot pozitív előjelű távolságnak vesszük, akkor az távolság levonó átkörzésével előáll a pozitív megoldás kétszerese, a 2x₁ távolság, (ezt a gyököt szigorú görög mestereink is megtalálták). Ha a távolságot negatív előjelű távolságnak tekintjük, akkor az távolság hozzáfűző átkörzésével (-() + = -2x) előáll a negatív megoldás kétszerese, a 2x₂ távolság, az ábrán az MN távolság. Konkrét adatokkal: ha a derékszögű háromszög két befogója a és , akkor az átfogó értéke (); ebből levonva az -őt, akkor a maradék 2x-ből adódik. Ez az összefüggés - tisztán geometriai meggondolásokból adódóan - azt mutatja, hogy az x és az távolságok (vagy a 2x és az a távolságok) aranyarányban vannak egymással; x alsó aranyszomszédja az távolságnak, (vagy 2x alsó aranyszomszédja az a távolságnak). Ez azt jelenti, hogy az x és az távolságok ismeretében a szabályos ötszög, például a szabályos ötágú csillag, körzővel és vonalzóval megszerkeszthető. Ha az átfogó számértéke (), akkor ehhez -őt adva, a negatív 2x-ből adódik. Ez az összefüggés is azt mutatja, hogy az x és az távolságok aranyarányban vannak egymással, x felső aranyszomszédja az távolságnak, (vagy a 2x felső aranyszomszédja az a távolságnak). Aranyarányban lévő távolságok ismeretében a pitagóreusok titkos szimbóluma, a szabályos ötágú csillag - körzővel és vonalzóval - könnyedén megszerkeszthető. A 3. ábra érdekessége, hogy a szerkesztéssel kapott derékszögű háromszög átfogójának a hossza megegyezik a 2. ábrán lévő AB húr hosszával: ez azt jelenti, hogy egy szabályos háromszög felhasználásával elkészítve a 2. ábrát olyan adatokhoz juthatunk, amelyek segítségével szabályos ötszöget szerkeszthetünk (lásd a 4. ábra jobb oldali részét!).

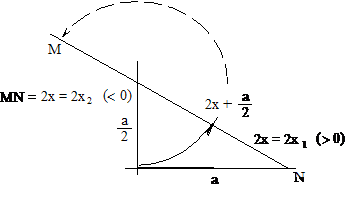
3. ábra. Az hiperbolikus egyenlet geometriai megoldásának vázlata; az a és az távolságok (a befogók) ismeretében a derékszögű háromszög megszerkeszthető, így a keresett x távolságot, egyenletünk gyökeit az hosszúságú befogó átfogóra történő kétszeri átkörzésével; levonó- és hozzáfűző elmetszésével kapott 2x₁ és 2x₂ távolságok megfelezésével kapjuk meg

A másodfokú egyenletek körzővel és vonalzóval történő megoldása roppant tanulságos dolog és számos érdekes következtetésre vezet (bővebben lásd [1]-et!). A most bemutatott speciális eset kapcsán bízom abban, hogy a leírtak alapján könnyen érthető dolgozatom furcsa címe, "kiindulva egy szabályos háromszögből, a 2. ábrán előállított x és távolságok segítségével könnyedén tudunk szabályos ötszöget szerkeszteni" (lásd a 4. ábra jobb oldali részét, az ábra önmagáért beszél).

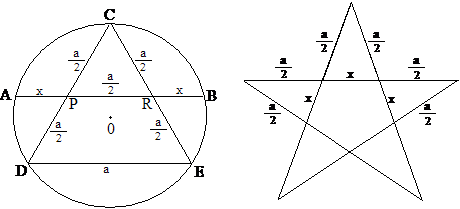
4. ábra. Az ábra bal oldali részén előállított x és távolságok segítségével a szabályos ötágú csillag (vagy a szabályos ötszög) körzővel és vonalzóval megszerkeszthető: "az ábra jobb oldali része önmagáért beszél"

Irodalom

[1] RINGLER A., 2003, Gondolkozzunk görögül, A Matematika Tanítása, Mozaik, XI. évfolyam, 5. szám, 3-8.

Dr. habil. Ringler András Ph.D.

egyetemi docens