Ringler András

A pitagorászi triplettek paritási tulajdonságai

„A tudományok királynője a matematika, a királynő koronája a számelmélet, a korona legszebb gyémántja pedig a négyzetes reciprocitás-tétel.” (Gauss)

A Püthagorasz-tétel örök téma. A Püthagorasz-tétel mindig aktuális. A Püthagorasz-tételre mindenki odafigyel. Ezt a tételt minden kisiskolás ismeri és ismerték már a Püthagorasz előtti civilizációkban is ( [1] ). E tétellel kapcsolatos triplettek létezésének ténye, a számhármasok előállítási szabályának felismerése már nagyon régen izgatja a matematikusok fantáziáját. Gondolataik célja, megtalálni azokat az egész számokat, amelyek kielégítik az alakban adott egyenletet. A probléma kapcsán nyilvánvaló dolog, hogy elegendő a közös osztóval nem rendelkező, az ún. primitív megoldások felkutatása.

Proklos Diadokhos-tól (410-485) tudjuk, hogy az összefüggést kielégítő triplettek előállítására Püthagorasz talált egy heurisztikus szabályt ( [2] ):

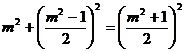amely könnyedén levezethető a magasság-tételből ( [3] ). Ebből a kifejezésből azonnal látszik, hogy a formulát kielégítő egész számhármasokat csak páratlan m számokkal lehet előállítani, hiszen páros m számok esetén a zárójeleken belüli hányadosok értéke nem lesz egész szám. Ezek az állítások könnyen felismerhetőek a számmisztikusok módszere alapján: az egymást követő páratlan számok alá írva az egymást követő számok négyzeteit, az így kapott elrendezésből látszik, hogy az első sorból kiválasztott bármelyik páratlan szám és az alatta lévő négyzetszám összege egyenlő az alsó sorban lévő négyzetszám jobb oldalán lévő négyzetszámmal. A dolog különösen érdekes akkor, ha az első sorból kiválasztott páratlan szám maga is négyzetszám; pl. 9, 25, 49, 81, 121, … . Az ilyen esetekhez tartozó összetartozó számhármasokat (9, 16, 25; 25, 144, 169; 49, 576, 625) az elrendezésben „vastagítva” tüntettem fel:

1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 …

0 1 4 9 16 25 36 49 64 81 100 121 144 169 196 225 256 289 324 361 400 441 484 529 576 625 676 ...

Ha az m szám csak páratlan szám lehet, akkor felmerül a kérdés, vajon az és az hányadosok milyen paritásúak? Könnyű megmutatni, hogy a formulát kielégítő pitagorászi triplettek esetén a páratlan m számhoz tartozó hányados csak páros, az hányados pedig csak páratlan szám lehet. Ez a szabály mindig igaz, vagyis más lehetőség nem valósulhat meg. Ha az m szám páratlan egész szám, akkor az szorzat biztosan osztható 8-cal, ezért az hányados osztható 4-gyel, az hányados tehát biztosan páros szám (a pitagorászi triplettek közötti egyetlen páros szám, amely 4-gyel biztosan osztható). Az páros szám azonban 4-gyel biztosan nem osztható, tehát csak 2-vel osztható; az szám tehát csak páratlan szám lehet. Ezen állítások bizonyítása indirekt módon is történhet. Tegyük fel, hogy az hányados nem páratlan, hanem alakú páros szám. Ebből , vagyis a feltételezésből páratlan m szám adódik, és ez így van jól (ez még nem ellentmondás!). Az feltételezésből az számra

adódik. Beírva -et, -et és az -et a pitagorászi triplett szabályba

adódik; tehát az egyenlőség fennáll: két páratlan szám összege párosat ad; a paritások alapján tehát az egyenlőség fennállhat! Mivel az m szám páratlan, tehát alakú, ezért . Mivel is fennáll, ezért , ami viszont gyönyörű lehetetlenség, hiszen e kifejezés bal oldala páros, a jobb oldalán viszont páratlan szám áll. Ez az ellentmondás nyílván azt jelenti, hogy a kiindulási feltételezés hamis, az hányados párossága tehát nem teljesülhet; páratlan m számok esetén ezért az hányados csak alakú páratlan szám lehet. Ebből adódik, tehát pártalan m számok esetén, az alakú számoknak párosnak kell lennie; qed. Ebben a gondolatsorban az ellentmondás abból adódott, hogy két, alakú páratlan szám összege sohasem adhat 4-gyel osztható páros számot.

A triplettek előállítására - az amerikai Columbia Egyetemen (New York) őrzött agyagtábla (a Plimpton 322 tábla) tanúsága szerint - a babilóniaiak is ismertek szabályt ( [4] ):

amelyből 4-gyel történő végigosztással és az behelyettesítésével előáll a pitagorászi triplett-szabály.

A triplettek általános paritásvizsgálata

Ha az összefüggést kielégítő a, b és c egész számoknak létezne közös osztója, akkor a legnagyobb közös osztó négyzetével végigosztva a kifejezést, egy „egyszerűbb összefüggéshez” jutunk. Ha ezután, az a, a b és a c egész számok közül bármelyik kettőnek lenne további közös osztója, akkor ez az osztó, osztója lenne a harmadik számnak is (ezen utóbbi állítást viszonylag könnyű belátni); ezért ezen közös osztó négyzetével történő újabb végigosztással tovább egyszerűsíthető a kifejezés. A végigosztásokkal kapott egyszerűsített kifejezés tagjairól következményként állíthatjuk, hogy

A. a három tag egyidejűleg nem lehet páros,

B. a három tag közül kettő sem lehet páros.

A B. eset (bár ez következmény) helyessége könnyen belátható, hiszen bármelyik két tag párossága esetén az kifejezés bal és jobb oldalainak paritása különböző, vagyis az egyenlőség nem állhat fenn. A végigosztásokkal kapott kifejezés tagjairól azonban még azt is állíthatjuk, hogy

C. mind a három tag nem lehet páratlan,

D. a három tag között csak egy páros tag léphet fel.

Ha mind a három tag páratlan lenne, akkor az kifejezés bal oldala páros, a jobb oldal pedig páratlan lenne. Ezen ellentmondás miatt a C. eset igaz. Mivel az A., a B. és a C. esetek mindegyike igaz (hamisságuk ellentmondásra vezet), ezért csak a D. eset igaz vagy hamis voltát kell ellenőrizni. Ha igaz a D. állítás, vagyis az a, a b és a c egész számok között, egy és csak egy páros szám lehet, akkor felmerül a kérdés; vajon melyik az?

Állítás: A primitív pitagorászi triplettek közötti legnagyobb szám, a c szám, csak páratlan lehet.

A bizonyítás indirekt. Tegyük fel, hogy az kifejezésben csak a c szám páros, vagyis alakú. Mivel a páratlan számok négyzete mindig (mod 8), ezért az kifejezés

alakba írásával „gyönyörű ellentmondás” látszik: az utóbbi kifejezés bal oldala páratlan, a jobb oldala viszont páros. Ezen ellentmondás miatt a primitív pitagorászi triplettek között fellépő egyetlen páros szám csak a két kisebbik szám egyike lehet. Ezek igazolják a kiinduláskor felvetett állítást: ha az

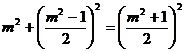
alakú Püthagorasz-tételt kielégítő triplettek egyike, pl. az m szám páratlan, vagyis a kifejezés bal oldalán az egyik tag, az páratlan; akkor a kifejezés másik tagja, az hányados csak páros szám (mégpedig 4-gyel is osztható páros szám) lehet; ezek miatt a triplett legnagyobb tagja, az hányados, csak páratlan szám lehet.

Összefoglalás: a (primitív) pitagorászi triplettek között fellépő egyetlen páros szám mindig osztható néggyel, és ez a szám - nagyság szerint - mindig a középső.

Irodalom

[1] Simonyi K.: A fizika kultúrtörténete, Akadémiai Kiadó, 1998.

[2] Lévárdi L. és Sain M.: Matematikatörténeti feladatok, Tankönyvkiadó, Budapest, 1982.

[3] Ringler A.: Püthagoraszi üzenet, A Matematika Tanítása, Mozaik Oktatási Stúdió, Szeged, 2002, X. évfolyam 3.

[4] Filep L.: A tudományok királynője, Bessenyei Kiadó, Nyíregyháza, 1997.

Kérdések

Egész számokkal miért nem állhat fenn a alakú egyenlőség?

Szeged, 2007. augusztus 6. Dr. Ringler András