Ringler András

Másodfokú egyenletek görög megoldása

és

a módszer általánosítása

A matematika fejlődésének nyomon követése, az emberi gondolkodás történetének bemutatása nagyon fontos és érdekes feladat. Annak ellenére, hogy minden tanár tudja, hogy tudománytörténeti kérdések felvetésével számos érdekes és hasznos ismeretet adhatunk át diákjainknak, mégis kevés időt áldozunk erre az iskolai munka során. Ez különösen igaz a matematika tanítására, pedig a matematikai gondolkodás fejlődésének bemutatása számos intellektuális öröm forrása. A görögök ezeréves matematikája mindenkit elbűvöl, nem győzünk eleget csodálkozni azon, hogy Eukleidész korában körzővel és vonalzóval oldották meg a másodfokú egyenleteket, és hogy geometriailag igazolták pl. az

(a + b)× (a - b) = a² - b²

nevezetes szorzatot is. Ezen persze nem kellene csodálkoznunk, hiszen a „görögök idejében” a matematikában jelentkező, gyakran válságot okozó problémákat egyszerűen áttolták a geometria körébe. Nem csoda hát, hogy 2000 évvel ezelőtt a geometria volt a legfontosabb tudomány. Ezt a gondolatot tükrözi a platoni Akadémia kapuja fölötti felirat is: „Ne lépjen be ide az, aki nem ismeri a geometriát”.

Az a× x – x² = b² alakú egyenletek körzővel és vonalzóval történő megoldásának leírásával már találkoztam, és mondhatom, roppant tanulságos volt a 2000 éves módszerrel való találkozás ([1]). A dolog megértése után kíváncsi lettem arra, vajon hogyan oldhatták meg a görögök az

a× x + x² = b², az a× x = b², és az a× b = x²

alakú, sőt az

a× x – x² = - b² és az a× x + x² = - b²

alakú egyenleteket. Megoldást bárki találhat, én is találtam, ezért ezeket kellő előkészítés után közreadom. (Figyelem! Az utóbbi két egyenletet a görögök nem tudták megoldani.)

Filep László „A tudományok királynője” című könyvéből megtudhatjuk, hogy a görögök miért, és hogyan geometrizálták a matematikát, és hogy - Eukleidész módszerét követve - hogyan oldották meg geometriailag az

a× x – x² = b²

alakú egyenleteket. E kifejezésben lévő a és b betűk előre megadott számok, az akkori szóhasználattal: mennyiségek, általában szakaszok. Az ilyen alakú kifejezéseket a görögök elliptikus sumptoma-nak, elliptikus feltételnek, mai szóhasználattal elliptikus egyenletnek nevezték. Ezen furcsa elnevezés hátterében a görögök mindent átható geometriai szemlélete, a kifejezésben lévő tagok geometriai megjelenítése áll. A görögök gondolkodása szerint ugyanis az a× x, az x² és a b² tagok rendre egy a és x oldalú téglalap, egy x oldalú négyzet, és egy b oldalú négyzet területeit képviselik. Az egyenlet megoldásakor keresték az a oldalhoz illeszthető téglalapok közül azt, amelynek x magasságával számolt a× x területéből elhagyva az x oldalú négyzet x² területét, maradékként éppen a b oldalú négyzet b² területe adódik. Igen-igen valószínű, hogy Eukleidész ezt valahogy így mondhatta: az a× x területű téglalap területét, x² terület-hiánnyal, b² területű négyzetté alakítom. Ezt a terület-hiánnyal történő téglalapillesztést a görögök elliptikus illesztésnek nevezték el (az elleipsis szó hiányt jelent!).

Az a× x + x² = b² alakú egyenlet megoldásánál a következő problémával állunk szemben: az a oldalhoz illeszthető téglalapok közül keressük annak a magasságát, amelynek a× x területéhez adva az x oldalú négyzet x² területét, megkapjuk a b oldalú négyzet b² területét. Eukleidész ezt valahogy így mondhatta: az a× x területű téglalap területét, x² terület-többlettel, b² területű négyzetté alakítom. Ezt a terület-többlettel történő illesztést a görögök hiperbolikus illesztésnek nevezték (a hiperbole szó többletet jelent!).

Az a× x = b² alakú egyenlet megoldásánál nincs szükség a terület-hiánnyal vagy a terület-többlettel történő illesztésre. Itt az a oldalhoz, hiány és többlet nélkül, vagyis megegyezésben - görögül parabolikusan - illesztjük a b²-tel megegyező területű, x magasságú téglalapot. Ezt a megegyezésben történő téglalapillesztést a görögök parabolikus illesztésnek nevezték (a parabole szó sem hiányt, sem többletet jelent, a görögök ezzel a szóval a megegyezésben történő illesztésre utaltak!).

Az a× b = x² alakú egyenlet megoldásához meg kell keresni annak a négyzetnek az x oldalát, amelynek x² területe megegyezik az a és a b oldalakból „készített” téglalap a× b területével. Az ilyen illesztés geometriai végrehajtása, az ismeretlen x oldal - körzővel és vonalzóval történő - megszerkesztése roppant egyszerű, ezért ezzel kezdem a megoldások bemutatását. Mivel x mértani közepe a-nak és b-nek, ezért x megszerkesztéséhez a magasság-tételt kell csak felidézni. Az a és a b szakaszok összeadása után megszerkesztjük az a + b szakasz köré rajzolható kört, és a derékszögű háromszög x magassága megadja a keresett négyzet oldalának hosszát (lásd az 1. ábrát!).

1. ábra. Az x² = a ·b egyenlet geometriai megoldásának lépései: az adott a és a b szakaszokból megszerkeszthető az a + b szakasz köré rajzolható kör. A magasság-tétel szerint a berajzolt x magasság a keresett illesztő négyzet oldala

A parabolikus, az elliptikus és a hiperbolikus illesztések menetét, az ilyen egyenletek geometriai megoldását a 2., a 3. és a 4., majd az 5. és 6. ábrák szemléltetik.

2. ábra. A parabolikus illesztés megoldásának lépései: az adott a és a b szakaszokból megszerkeszthető a berajzolt kör középpontja, a kör megrajzolásával adódik a parabolikusan illesztő téglalap x magassága, hiszen a magasság-tétel szerint: b² = a · x

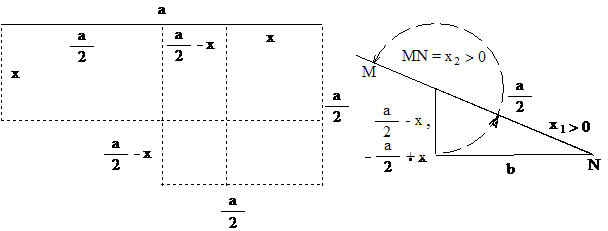
3. ábra. Az elliptikus illesztés és a keresett x oldal szerkesztésének lépései. A megoldhatóság feltétele: az a/2 hosszúságú átfogó legyen nagyobb, mint a b hosszúságú befogó. Az a× x – x² = b² alakú elliptikus szümptómának negatív megoldása nem lehet

Az a× x – x² = b² alakú elliptikus szümptóma geometriai megoldásának felismeréséhez a 3. ábrán az előre megadott a oldalhoz x magasságú téglalapot rajzolunk (ne zavarjon senkit, hogy x-et nem ismerjük!), és az a oldal jobboldali végéről visszamérjük a nem ismert x távolságot. Rajzoljunk az a szakasz jobb oldali végéhez egy a/2 oldalhosszúságú négyzetet, lásd a 3. ábra baloldali részét! A berajzolt szaggatott vonalakkal kapott kis négyszögek megfelelő oldalainak a hosszát az ábra mutatja, segítségükkel bármelyik kis négyszög területe kiszámolható. Éppen ezekre lesz szükségünk. Számítsuk ki a berajzolt a/2 oldalhosszúságú négyzet területét az őt alkotó kis négyszögek területeinek összegeként, és használjuk fel, hogy a · x - x² = b²:

.

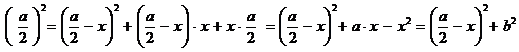Ebből máris látszik x szerkeszthetősége, hiszen eredményünk azt mutatja, hogy az a/2, az (a/2 – x) és a b mennyiségek között pitagorászi összefüggés áll fenn. Ha az a/2 átfogó nagyobb mint a b befogó, akkor velük a 3. ábrán látható derékszögű háromszög mindig megszerkeszthető, így a szerkesztéssel előáll az (a/2 - x) hosszúságú befogó, amely „tartalmazza” a keresett x távolságot (lásd a 3. ábra jobboldali részét!). Ezt a szerkesztéssel kapott (a/2 - x) távolságot (a gyökvonás kétértékűsége miatt először pozitívnak, majd negatívnak kell tekinteni!). Az a/2 - x hosszúságú befogót levonva az a/2 hosszúságú átfogóból, az ún. levonó átkörzéssel megkapjuk az elliptikusan illesztő téglalap nem ismert x magasságát: a/2 - (a/2 - x) = x. Ez a pozitív megoldás lesz az elliptikus egyenlet első megoldása, az x₁. Az ábráról az is látszik, hogy a „leolvasott megoldás” a/2-nél kisebb lesz. A szerkesztő ábra azonban az a/2-nél nagyobb megoldás megtalálásához is felhasználható. Ehhez az (a/2 - x) befogót negatívnak gondoljuk (bár a görögök nem tudtak volna mit kezdeni azzal, hogy az (a/2 - x) szakasz előjele negatív), így értéke (- a/2 + x). Az egyenlet második megoldásának megtalálásához az (a/2 - x) befogó átkörzését ne hagyjuk abba az a/2 hosszúságú átfogó első elmetszésénél, hanem „haladjunk tovább”, és metsszük el az átfogó meghosszabbítását az M pontnál (lásd a 3. ábra jobb oldalát!), így a második megoldást az a/2 hosszúságú átfogó és a (- a/2 + x) hosszúságú befogó összege adja; az a/2 + (– a/2 + x) összeg tehát „megadja” az elliptikus egyenlet második megoldását, az x₂-őt (x₂ º MN) és ez a megoldás is pozitív lesz. De ennek így is kell lennie, az a× x – x² = b² alakú elliptikus szümptóma geometriai megoldásánál mindig két pozitív gyököt kell kapni; hiszen az ilyen egyenletnek negatív megoldása nem is lehet; negatív x esetén a szümptóma bal oldala negatív lenne, a jobb oldala viszont pozitív.

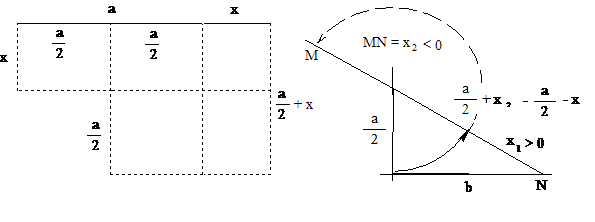
4. ábra. A hiperbolikus illesztés és a keresett x oldal szerkesztésének lépései. A megoldhatóságnak nincs feltétele

Az a× x + x² = b² alakú hiperbolikus szümptóma geometriai megoldásának felismeréséhez a 4. ábrán az előre megadott a oldalt meghosszabbítjuk a nem ismert illesztő téglalap x magasságával (nem baj, hogy nem ismerjük!), és megrajzoljuk az a + x szakaszhoz az x magasságú illesztő téglalapot. Rajzoljunk az a + x szakasz jobb oldali végéhez egy a/2 + x oldalhosszúságú négyzetet, lásd az ábra bal oldali részét! A berajzolt szaggatott vonalakkal kapott kis négyszögek megfelelő oldalainak a hosszát az ábra mutatja, segítségükkel bármelyik kis négyszög területe kiszámolható. Éppen ezekre lesz szükségünk. Számítsuk ki a berajzolt a/2 + x oldalhosszúságú négyzet területét az őt alkotó kis négyszögek területeinek összegeként, és használjuk fel, hogy a · x + x² = b²:

.

Ebből máris látszik x szerkeszthetősége, hiszen eredményünk azt mutatja, hogy az (a/2 + x), az a/2 és a b mennyiségek között pitagorászi összefüggés áll fenn: a b és az a/2 befogókkal derékszögű háromszöget szerkesztve megkapjuk az (a/2 + x) hosszúságú átfogót (lásd a 4. ábra jobb oldali részét!). A szerkesztéssel kapott (a/2 + x) átfogóra az a/2 hosszúságú befogót átkörözve, levonó átkörzéssel, levonással megkapjuk a hiperbolikusan illesztő téglalap nem ismert x magasságát: (a/2 + x) - a/2 = x º x₁; és az így előállt távolság lesz a hiperbolikus egyenlet első gyöke, mégpedig pozitív gyöke. A kapott szerkesztő ábra azonban használható egyenletünk negatív gyökének a megtalálásához is. Ehhez, ne hagyjuk abba az a/2 hosszúságú befogó átfogóra történő átkörzését az első elmetszésnél, hanem „haladjunk tovább”, és metsszük el az átfogó meghosszabbítását az M pontnál (lásd a 4. ábra jobb oldali részét!). A gyökvonás kétértékűsége miatt most az átfogót negatívnak tekintjük, így a (- a/2 - x) hosszúságúnak gondolt átfogó és a rá felmért a/2 szakasz összege adja meg a hiperbolikus egyenlet másik, a negatív előjelű megoldását: (- a/2 - x) + a/2 = - x º - x₂ (º MN).

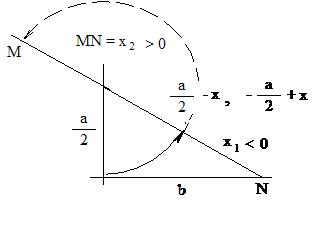
5. ábra. Az a× x – x² = - b² alakú elliptikus szümptóma geometriai megoldásának lépései. A megoldhatóságnak nincs feltétele

A módszer általánosítása

Az a× x – x² = b² és az a× x + x² = b² alakú egyenletek geometriai megoldásának általánosításaként engedjük meg az egyenletek jobb oldalán a „- b²” alakú tag fellépését is. Természetesen ezt a görögök meg nem engedhető dolognak tartották. Ekkor az a× x – x² = - b² elliptikus szümptóma geometriai megoldásának felismeréséhez a fenti

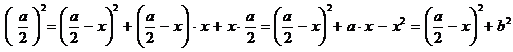
kifejezésben az a× x – x² helyére „- b²”-et kell behelyettesíteni, ekkor

adódik, amelyből látható, hogy az a/2, a b és az (a/2 - x) mennyiségek között pitagorászi összefüggés áll fenn. Az a/2 és a b befogókkal a derékszögű háromszög megszerkeszthetőségének nincsen semmilyen akadálya, ezért az (a/2 - x) hosszúságú átfogó előállítható (lásd az 5. ábrát!). Most az átfogó hosszát a gyökvonás kétértékűsége miatt (a/2 - x)-nek, illetve (-a/2 + x)-nek kell tekinteni. Azonnal látszik, hogy az a/2 hosszúságú befogó levonó átkörzésével, (a/2 - x) - a/2 = - x₁, negatív megoldást kapunk; a hozzáfűző átkörzéssel pedig, (-a/2 + x) + a/2 = x₂ º MN, pozitív megoldás adódik.

Az a× x + x² = - b² hiperbolikus szümptóma geometriai megoldásának felismeréséhez a fenti

kifejezésben az a× x + x² helyére „- b²”-et kell behelyettesíteni, ekkor

adódik, amelyből látható, hogy az (a/2 + x) , a b és az a/2 mennyiségek között pitagorászi összefüggés áll fenn. Ha az a/2 átfogó nagyobb mint a b befogó, akkor a derékszögű háromszög megszerkeszthető, így az (a/2 + x) hosszúságú befogó előállítható és ez a távolság magába foglalja a kereset ismeretlen távolságot (lásd a 6. ábrát!). Most e befogó hosszát a gyökvonás kétértékűsége miatt (a/2 + x)-nek, illetve (- a/2 - x)-nek kell tekinteni. Azonnal látszik, hogy a befogó átfogóból történő levonó átkörzésével, a/2 - (a/2 + x) = - x º - x₁, negatív megoldást kapunk; de a hozzáfűző átkörzéssel is, a/2 + (- a/2 - x) = - x₂ º MN, negatív megoldás adódik. De ennek így is kell lennie, az a · x + x² = - b² alakú hiperbolikus szümptómának pozitív megoldása nyílván nem is lehet, hiszen ekkor a bal oldala pozitív, a jobb oldala viszont negatív volna.

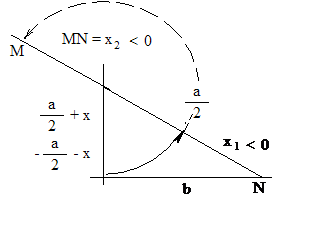
6. ábra. Az a× x + x² = - b² alakú hiperbolikus szümptóma geometriai megoldásának lépései. A megoldhatóság feltétele: az a/2 hosszúságú átfogó legyen nagyobb, mint a b hosszúságú befogó. Az ilyen egyenletnek pozitív megoldásai nem lehetnek

A másodfokú egyenletek megoldásának diszkussziója során a görögök a negatív megoldásokkal nem törődtek, nem is keresték őket, Ők nem ismerték a negatív számokat, nem tudtak nekik szemléletes jelentést adni: gondolatilag nem tudtak mit kezdeni például egy negatív kecske, vagy egy negatív szakasz fogalmával. A negatív szám, a negatív mennyiség nem létezett a számukra. A negatív szám fogalma csírájának nyomait csakis a valódinak tekintett mennyiségek csökkenéseinél, kiadásoknál, valamiféle hiány, vagy valamilyen adósság fellépteként ismerhetjük fel. Bár a görögöknek volt külön jelük a kivonás műveletére, de ezt nem előjelnek, hanem műveleti jelnek tekintették. Ez, és túlzott geometriai szemléletük az oka annak, hogy a másodfokú egyenleteket nem algebrailag, hanem geometriailag oldották meg. A görögök matematikáján való töprengés érdekes gondolati lavinát indíthat el az emberben. Bárkiben felmerülhet a kérdés, vajon hogyan és milyen irányban fejlődött volna a görögök matematikája, ha ezeréves matematikai kultúrájuk továbbfejlődését a kereszténység és az iszlám terjeszkedése nem akadályozta volna. Mi lett volna akkor, ha 529-ben a keresztény bizánci Justinianus nem záratta volna be az athéni Akadémiát; vagy mi lett volna akkor, ha az arab terjeszkedés alatt, 641-ben Omár kalifa nem gyújtatta volna fel az alexandriai könyvtárat és egyetemet. Sajnálatos tény, de ezen események után számos okos ember nézet más haza után, a görög tudósok „szétszéledtek”. Nem véletlen, hogy a tudománytörténészek éppen ettől az időszaktól számítják a történelmi középkort.

A másodfokú egyenletekkel kapcsolatosan az elliptikus, a hiperbolikus és a parabolikus illesztések gondolatát Eukleidész vetette fel és oldotta meg, de az ellipszis, a hiperbola és a parabola matematikába történő bevezetése Appolóniusz nevéhez fűződik. Dolgozatommal, a több mint 2000 éves gondolatok felelevenítésével, tisztelettel adózom valamennyiünk görög mestereinek, a geometria óriásainak, Eukleidésznek és Appolóniusznak.

A dolgozatban bemutatott módszer érdekessége abban „áll”, hogy használatával geometriai úton kapjuk meg a bemutatott másodfokú egyenlet(ek) második megoldását is; az általánosított módszer olyan szümptómák megoldására is használható, amilyeneket a görögök nem tudtak megoldani.

Irodalom

[1] Filep László: A tudományok királynője, 1997, TYPOTEX Kft. - Budapest, Bessenyei Kiadó - Nyíregyháza, ISBN 963 7546 83 9.

[2] Simonyi Károly: A fizika kultúrtörténete, 1998, Akadémiai Kiadó, ISBN 963 05 7651 2.

[3] Ringler András: Mi köze van a szabályos háromszögnek a szabályos ötszöghöz, 2004, A Matematika Tanítása, Mozaik Oktatási Stúdió, Szeged, XII. évfolyam, 4. szám, 3-7.

[4] Ringler András: A , 2003, A Matematika Tanítása, Mozaik Oktatási Stúdió, Szeged, XI. évfolyam, 2. szám, 17-23.

[5] Ringler András: Gondolkozzunk „görögül”, 2003, A Matematika Tanítása, Mozaik Oktatási Stúdió, Szeged, XI. évfolyam, 5. szám, 3-8.

Feladatok

1. Oldja meg geometriailag a 16·x = 64 parabolikus egyenletet! (x = 4).

2. Oldja meg geometriailag a 20·x – x² = 64 elliptikus egyenletet! (x₁ = 4 és x₂ = 16).

3. Oldja meg geometriailag a 12·x + x² = 64 hiperbolikus egyenletet! (x₁ = 4 és x₂ = -16).

4. Oldja meg geometriailag a 12·x – x² = – 64 (elliptikus) egyenletet! (x₁ = 16 és x₂ = – 4 ).

5. Oldja meg geometriailag a 20·x + x² = – 64 (hiperbolikus) egyenletet! (x₁ = – 4 és x₂ = –16).

6. Oldja meg geometriailag Brahmagupta (598, 660) híres, 10×x + x² = 39 alakban megadott (hiperbolikus) egyenletét is! (x₁ = 3 és x₂ = -13). Brahmagupta, a teljes négyzetté történő kiegészítéssel, csak az x₁ = 3 megoldást találta meg.

-->