Ringler
András
Gondolkozzunk
„görögül”!
Másodfokú egyenletek geometriai megoldása
A
matematika fejlődésének nyomon követése, az emberi gondolkodás történetének
bemutatása nagyon fontos és érdekes feladat. Tudománytörténeti kérdések
felvetésével számos érdekes és hasznos ismeretet adhatunk át tanítványainknak; a régi dolgok újragondolása -
a harmóniák felismerése -
számos intellektuális öröm forrása. Pl. a görögök ezeréves matematikája
mindenkit elbűvöl, én nem győzök eleget csodálkozni azon, hogy Euklidész
korában körzővel és vonalzóval oldották meg a másodfokú egyenleteket. Ezen
persze nem kellene csodálkozni, hiszen a „görögök idejében” a matematikában
jelentkező, gyakran válságot okozó problémákat egyszerűen „áttolták” a
geometria körébe: nem csoda hát, hogy »2000 évvel ezelőtt a geometria volt a
„fő-tudomány”. Ezt a gondolatot tükrözi a platóni Akadémia kapuján lévő felirat
is: „Ne lépjen be ide az, aki nem ismeri a geometriát”.
Az a×x – x2 = b2,
az a×x + x2 = b2,
az a×x = b2 és az
a×b = x2 alakú egyenletek körzővel és vonalzóval
történő megoldása roppant tanulságos (lásd [1]-et és [2]-őt). E kifejezésekben lévő a
és b betűk előre megadott számok, az akkori szóhasználattal:
mennyiségek, általában szakaszok. Az a×x – x2 = b2 alakú kifejezéseket a görögök elliptikus sumptoma-nak, elliptikus feltételnek, mai
szóhasználattal elliptikus egyenletnek nevezték. Ezen furcsa elnevezés
hátterében a görögök mindent átható geometriai szemlélete, a kifejezésekben
lévő tagok geometriai megjelenítése áll. A görögök gondolkodása szerint ugyanis
az a×x,
az x2 és a b2 tagok rendre egy a és x
oldalú téglalap, egy x oldalú négyzet, és egy b oldalú négyzet
területeit képviselik. Az a×x – x2 = b2 alakú egyenlet megoldásakor keresték az a
oldalhoz illeszthető téglalapok közül azt, amelynek x magasságával
számolt a×x területéből
elhagyva az x oldalú négyzet x2 területét, maradékként
éppen a b oldalú négyzet b2 területe adódik. Igen-igen
valószínű, hogy Euklidész ezt valahogy így mondhatta: az a×x területű téglalap területét, x2
terület-hiánnyal, b2 területű négyzetté alakítom. Ezt a
terület-hiánnyal történő „téglalapillesztést” a görögök elliptikus illesztésnek
nevezték.
Az a×x + x2 = b2 alakú egyenlet megoldásánál a következő
problémával állunk szemben: az a oldalhoz illeszthető téglalapok közül
keressük annak a magasságát, amelynek a×x területéhez adva az x oldalú négyzet x2
területét, megkapjuk egy b oldalú négyzet b2
területét. Euklidesz ezt valahogy így mondhatta: az a×x területű téglalap területét, x2
terület-többlettel, b2 területű négyzetté alakítom. Ezt a
terület-többlettel történő „téglalapillesztést” a görögök hiperbolikus
illesztésnek nevezték.
Az a×x = b2 alakú egyenlet megoldásánál nincs szükség a
terület-hiánnyal vagy a terület-többlettel történő illesztésekre. Itt az a
oldalhoz, hiány és többlet nélkül, vagyis megegyezésben -
görögül parabolikusan -
illesztjük a b2-tel megegyező területű, x magasságú
téglalapot. Ezt a megegyezésben történő „téglalapillesztést” a görögök
parabolikus illesztésnek nevezték. Az a×x = b2 alakú egyenletek körzővel és vonalzóval
történő megoldása roppant egyszerű, például a magasság-tétellel: az adott a
és az ismeretlen x távolság mértani közepe a (szintén adott) b
távolság. Az a×b = x2 alakú egyenlet megoldása is roppant egyszerű,
hiszen itt x2 mértani közepe az a és a b távolságoknak.
A
másodfokú egyenletek megoldásának diszkussziója során a görögök a negatív
megoldásokkal nem törődtek, hiszen nem ismerték a negatív számokat, nem tudtak
nekik szemléletes jelentést adni: gondolatilag nem tudtak mit kezdeni például
egy negatív kecske, vagy egy negatív szakasz fogalmával. A negatív szám, a
negatív mennyiség nem létezett a számukra. A görögöknél a negatív szám fogalma
csírájának nyomait csakis a valódinak tekintett mennyiségek csökkenéseinél,
kiadásoknál, valamiféle hiány, vagy valamilyen adósság fellépteként ismerhetjük
fel. Bár a görögöknek volt külön jelük a kivonás műveletére, de ezt nem
előjelnek, hanem műveleti jelnek tekintették. Ez, és túlzott geometriai
szemléletük az oka annak, hogy a másodfokú egyenleteket nem algebrailag, hanem
geometriailag oldották meg ([3]).
A
másodfokú egyenletekkel kapcsolatosan az elliptikus, a hiperbolikus és a
parabolikus illesztések gondolatát Euklidész vetette fel és oldotta meg, de az
ellipszis, a hiperbola és a parabola matematikába történő bevezetése
Appolóniusz nevéhez fűződik. Dolgozatommal, a több mint 2000 éves gondolatok
felelevenítésével, tisztelettel adózom valamennyiünk görög mestereinek, a
geometria óriásainak, Euklidésznek és Appolóniusznak. Az Ő és kortársaik
gondolatainak köszönhetjük, hogy természetfilozófiai szemléletünk gyökerei
viszonylag hamar kialakultak ([4]).
A
görögök matematikáján való töprengés érdekes gondolati lavinát indíthat el.
Bárkiben felmerülhet a kérdés, vajon hogyan és milyen irányban fejlődött volna
a görögök matematikája, ha ezeréves matematikai kultúrájuk továbbfejlődését a
kereszténység és az iszlám terjeszkedése nem akadályozta volna. Mi lett volna
akkor, ha 529-ben a bizánci Justinianus nem záratta volna be az athéni
Akadémiát; vagy mi lett volna akkor, ha az arab
terjeszkedés alatt, 641-ben Omár kalifa nem gyújtatta volna fel az alexandriai
könyvtárat és egyetemet. Sajnálatos tény, de ezen események után számos okos
ember nézett más haza után, a görög tudósok „szétszéledtek”. Nem véletlen, hogy
a tudománytörténészek ettől az időszaktól számítják a történelmi középkort ([5]).
Az a×x – x2 = b2 és az
a×x + x2
= b2 alakú egyenletek [1]-ben leírt -
kissé heurisztikus -
megoldása kapcsán elgondolkozhatunk azon, vajon hogyan oldották volna
meg a görögök az ilyen sumptoma-kat, ha az egyenletek jobb oldalán
negatív szám, vagyis – b2 állna? Bár a görögök számára az
a×x – x2 = – b2 és az
a×x + x2
= – b2
alakú
egyenletek értelmetlenek voltak, hiszen számukra az x2
terület-hiánnyal és az x2 terület-többlettel történő
illesztés nem eredményezhet „negatív területű négyzetet”. Ennek ellenére
gondolkozzunk el azon, vajon hogyan lehetne az ilyen típusú egyenleteket – „mai
fejjel” – körzővel és vonalzóval megoldani. Hogy mire
jutottam, szívesen közreadom;
már csak azért is, mert „gyönyörű harmóniákat” és szimmetriákat ismerhetünk fel
az elmondottak mögött (lásd az ábrákat!). A görögök óta a „harmóniák keresése”
minden tudományterület legfontosabb hajtómotorja; a harmóniák felismerése mindig
lenyűgözi az embert.
A felvetett problémák geometriai
megoldása lehetőségének felismeréséhez az
a×x – x2
= – b2 illetve az a×x + x2 = – b2 alakú egyenleteket algebrailag – egy
kicsit –
át kell alakítani;
így roppant érdekes eredményekhez juthatunk: az egyenletek megoldhatóságának
feltételei is egyszerű geometriai tényekből adódnak; a megoldhatósági feltételek tehát nem
algebrailag, nem a diszkrimináns értékéből, hanem geometriai tényekből
állapíthatjuk meg. Jelen dolgozatomban leírt módszer kapcsán újból tárgyalom
az a×x – x2 = b2 és az
a×x + x2
= b2 alakú egyenletek
geometriai megoldását, mivel a most bemutatott módszer már nem olyan
heurisztikus, mint amelyet [1]-ben írtam le.
Az ![]() alakú kifejezés -
alakú kifejezés -
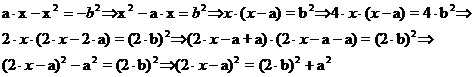
- átalakításaival azt kaptuk, hogy az a, a
2b és a 2x-a mennyiségek
között pitagorászi összefüggés áll fenn; vagyis a felsorolt mennyiségek egy
derékszögű háromszög oldalai (lásd az 1. ábrát!). Itt a szerkesztéssel kapott 2x-a hosszúságú átfogó "tartalmazza" a keresett x
távolságot. A gyökvonás kétértékűsége miatt a 2x-a mennyiséget egyszer pozitívnak, majd negatívnak kell
gondolnunk, így hosszát 2x-a-nak illetve -(2x-a)-nak kell venni.
Ha a 2x-a mennyiség pozitív, akkor az a távolság 2x-a átfogóra történő hozzáfűző átkörzésével, vagyis
hozzáadásával, előáll a 2x távolság (2x º MN), amelynek felezésével -
pozitív előjelű távolságként -
áll elő egyenletünk első, a (pozitív előjelű) x1
megoldása (ezt a hozzáfűző „trükköt” a görögök nem csinálták). Ha a 2x-a mennyiség negatív, akkor az a befogó hosszát, az
átfogó a-2x
hosszúságából, levonó átkörzéssel levonva, negatív előjelű 2x távolságot
kapunk, amelynek felezésével távolságként kapjuk meg egyenletünk másik, a
(negatív előjelű) x2 megoldását (lásd az 1. ábrát!).
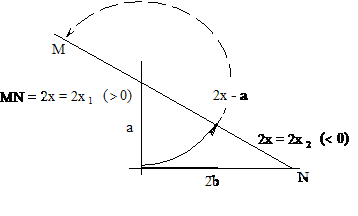
1. ábra.
Az ![]() alakú (elliptikus)
egyenlet geometriai megoldásának vázlata; az a és 2b távolságok
ismeretében a derékszögű háromszög megszerkeszthető, így az egyenlet gyökeit a
bejelölt 2x1 és 2x2 távolságok
megfelezésével kapjuk meg
alakú (elliptikus)
egyenlet geometriai megoldásának vázlata; az a és 2b távolságok
ismeretében a derékszögű háromszög megszerkeszthető, így az egyenlet gyökeit a
bejelölt 2x1 és 2x2 távolságok
megfelezésével kapjuk meg
Az 1. ábráról látszik, hogy a
derékszögű háromszög megszerkeszthetőségének, tehát az ![]() egyenlet
megoldhatóságának nincs semmilyen geometriai feltétele; de ennek így is kell lennie, hiszen
az ilyen alakú egyenlet diszkriminánsa, az a2 + 4b2
mindig pozitív. Ilyen esetekben mindig két gyököt, egy pozitív és egy negatív
gyököt várunk.
egyenlet
megoldhatóságának nincs semmilyen geometriai feltétele; de ennek így is kell lennie, hiszen
az ilyen alakú egyenlet diszkriminánsa, az a2 + 4b2
mindig pozitív. Ilyen esetekben mindig két gyököt, egy pozitív és egy negatív
gyököt várunk.
Az ![]() alakú kifejezés -
alakú kifejezés -
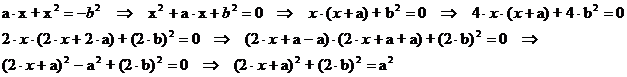 - átalakításaival azt kaptuk, hogy az a, a
2b és a 2x + a
mennyiségek között pitagorászi összefüggés áll fenn; vagyis a felsorolt mennyiségek egy
derékszögű háromszög oldalai (lásd a 2. ábrát!). Itt a szerkesztéssel kapott 2x+a
hosszúságú befogó "tartalmazza" a keresett x távolságot. A
gyökvonás kétértékűsége miatt a 2x+a mennyiséget egyszer pozitívnak,
majd negatívnak kell gondolnunk, így hosszát 2x+a-nak illetve -(2x+a)-nak kell venni.
- átalakításaival azt kaptuk, hogy az a, a
2b és a 2x + a
mennyiségek között pitagorászi összefüggés áll fenn; vagyis a felsorolt mennyiségek egy
derékszögű háromszög oldalai (lásd a 2. ábrát!). Itt a szerkesztéssel kapott 2x+a
hosszúságú befogó "tartalmazza" a keresett x távolságot. A
gyökvonás kétértékűsége miatt a 2x+a mennyiséget egyszer pozitívnak,
majd negatívnak kell gondolnunk, így hosszát 2x+a-nak illetve -(2x+a)-nak kell venni.
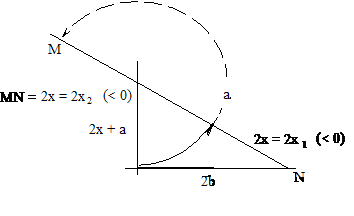
2. ábra. Az ![]() alakú (hiperbolikus)
egyenlet geometriai megoldásának vázlata; az ilyen alakú egyenleteknek pozitív
gyöke nem lehet. Az a és 2b távolságok ismeretében, a > 2b esetén a derékszögű háromszög megszerkeszthető, így az
egyenlet gyökeit a bejelölt 2x1 és 2x2 távolságok
megfelezésével kapjuk meg
alakú (hiperbolikus)
egyenlet geometriai megoldásának vázlata; az ilyen alakú egyenleteknek pozitív
gyöke nem lehet. Az a és 2b távolságok ismeretében, a > 2b esetén a derékszögű háromszög megszerkeszthető, így az
egyenlet gyökeit a bejelölt 2x1 és 2x2 távolságok
megfelezésével kapjuk meg
A 2. ábráról azonnal látszik, hogy a
derékszögű háromszög megszerkeszthetőségének, az ![]() egyenlet
megoldhatóságának geometriai feltétele: a > 2b, hiszen az a átlónak nagyobbnak kell lennie bármelyik
befogónál (így a 2x+a-nál is). Ezen megoldhatósági feltétel érdekessége
az, hogy ezt geometriai tényekből, és nem algebrai megfontolásokból kaptuk meg.
Egyenletünk algebrai megoldhatóságának jól ismert oka: az ilyen egyenlet
diszkriminánsa a2 - 4b2 > 0; ezért a megoldhatóság feltétele: a
>
2b. A 2. ábráról az
is látszik, hogy egyenletünk megoldása nem lehet pozitív mennyiség, különben az
a hosszúságú átfogó nem lenne nagyobb a másik, a 2x+a hosszúságú
befogónál. Ezt persze ránézéssel is tudhatjuk: az
egyenlet
megoldhatóságának geometriai feltétele: a > 2b, hiszen az a átlónak nagyobbnak kell lennie bármelyik
befogónál (így a 2x+a-nál is). Ezen megoldhatósági feltétel érdekessége
az, hogy ezt geometriai tényekből, és nem algebrai megfontolásokból kaptuk meg.
Egyenletünk algebrai megoldhatóságának jól ismert oka: az ilyen egyenlet
diszkriminánsa a2 - 4b2 > 0; ezért a megoldhatóság feltétele: a
>
2b. A 2. ábráról az
is látszik, hogy egyenletünk megoldása nem lehet pozitív mennyiség, különben az
a hosszúságú átfogó nem lenne nagyobb a másik, a 2x+a hosszúságú
befogónál. Ezt persze ránézéssel is tudhatjuk: az ![]() alakú egyenletnek
pozitív megoldása nem lehet, hiszen ilyen esetben a kiindulási egyenletünk bal
oldala pozitív lesz, a jobb oldalán viszont negatív szám áll. Ha a 2x+a
hosszúságú befogót (levonó átkörzéssel) levonjuk az a hosszúságú
átfogóból, akkor egy 2x hosszúságú „negatív” távolságot kapunk, amelynek
felezésével megkapjuk egyenletünk első (negatív előjelű) megoldását, az x1-et.
Egyenletünk másik megoldását az átfogó újbóli elmetszésével (az M pontnál)
állíthatjuk elő. Ha a 2x+a hosszúságú befogót (a negatív előjelű
befogót, hozzáfűző átkörzéssel) az a hosszúságú átfogóhoz adjuk (-(2x+a) + a = -2x), akkor egy 2x hosszúságú
„negatív” távolságot kapunk (2x º MN), amelynek felezésével megkapjuk
az
alakú egyenletnek
pozitív megoldása nem lehet, hiszen ilyen esetben a kiindulási egyenletünk bal
oldala pozitív lesz, a jobb oldalán viszont negatív szám áll. Ha a 2x+a
hosszúságú befogót (levonó átkörzéssel) levonjuk az a hosszúságú
átfogóból, akkor egy 2x hosszúságú „negatív” távolságot kapunk, amelynek
felezésével megkapjuk egyenletünk első (negatív előjelű) megoldását, az x1-et.
Egyenletünk másik megoldását az átfogó újbóli elmetszésével (az M pontnál)
állíthatjuk elő. Ha a 2x+a hosszúságú befogót (a negatív előjelű
befogót, hozzáfűző átkörzéssel) az a hosszúságú átfogóhoz adjuk (-(2x+a) + a = -2x), akkor egy 2x hosszúságú
„negatív” távolságot kapunk (2x º MN), amelynek felezésével megkapjuk
az ![]() alakú egyenlet másik,
a negatív előjelű megoldását, az x2-őt (ezt a hozzáfűző
„trükköt” a görögök nem csinálták!).
alakú egyenlet másik,
a negatív előjelű megoldását, az x2-őt (ezt a hozzáfűző
„trükköt” a görögök nem csinálták!).
Az ![]() alakú kifejezés -
alakú kifejezés -
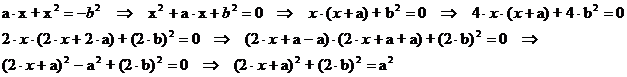 - átalakításaival azt kaptuk, hogy az a, a
2b és a 2x + a
mennyiségek között pitagorászi összefüggés áll fenn; vagyis a felsorolt mennyiségek egy
derékszögű háromszög oldalai (lásd a 2. ábrát!). Itt a szerkesztéssel kapott 2x+a
hosszúságú befogó "tartalmazza" a keresett x távolságot. A
gyökvonás kétértékűsége miatt a 2x+a mennyiséget egyszer pozitívnak,
majd negatívnak kell gondolnunk, így hosszát 2x+a-nak illetve -(2x+a)-nak kell venni.
- átalakításaival azt kaptuk, hogy az a, a
2b és a 2x + a
mennyiségek között pitagorászi összefüggés áll fenn; vagyis a felsorolt mennyiségek egy
derékszögű háromszög oldalai (lásd a 2. ábrát!). Itt a szerkesztéssel kapott 2x+a
hosszúságú befogó "tartalmazza" a keresett x távolságot. A
gyökvonás kétértékűsége miatt a 2x+a mennyiséget egyszer pozitívnak,
majd negatívnak kell gondolnunk, így hosszát 2x+a-nak illetve -(2x+a)-nak kell venni.

2. ábra. Az ![]() alakú (hiperbolikus)
egyenlet geometriai megoldásának vázlata; az ilyen alakú egyenleteknek pozitív
gyöke nem lehet. Az a és 2b távolságok ismeretében, a > 2b esetén a derékszögű háromszög megszerkeszthető, így az
egyenlet gyökeit a bejelölt 2x1 és 2x2
távolságok megfelezésével kapjuk meg
alakú (hiperbolikus)
egyenlet geometriai megoldásának vázlata; az ilyen alakú egyenleteknek pozitív
gyöke nem lehet. Az a és 2b távolságok ismeretében, a > 2b esetén a derékszögű háromszög megszerkeszthető, így az
egyenlet gyökeit a bejelölt 2x1 és 2x2
távolságok megfelezésével kapjuk meg
A 2. ábráról azonnal látszik, hogy a
derékszögű háromszög megszerkeszthetőségének, az ![]() egyenlet
megoldhatóságának geometriai feltétele: a > 2b, hiszen az a átlónak nagyobbnak kell lennie
bármelyik befogónál (így a 2x+a-nál is). Ezen megoldhatósági feltétel
érdekessége az, hogy ezt geometriai tényekből, és nem algebrai megfontolásokból
kaptuk meg. Egyenletünk algebrai megoldhatóságának jól ismert indoka: az ilyen
egyenlet diszkriminánsa a2 - 4b2, ezért a megoldhatóság feltétele: a
>
2b. A 2. ábráról az
is látszik, hogy egyenletünk megoldása nem lehet pozitív mennyiség, különben az
a hosszúságú átfogó nem lenne nagyobb a másik, a 2x+a hosszúságú
befogónál. Ezt persze ránézéssel is tudhatjuk: az
egyenlet
megoldhatóságának geometriai feltétele: a > 2b, hiszen az a átlónak nagyobbnak kell lennie
bármelyik befogónál (így a 2x+a-nál is). Ezen megoldhatósági feltétel
érdekessége az, hogy ezt geometriai tényekből, és nem algebrai megfontolásokból
kaptuk meg. Egyenletünk algebrai megoldhatóságának jól ismert indoka: az ilyen
egyenlet diszkriminánsa a2 - 4b2, ezért a megoldhatóság feltétele: a
>
2b. A 2. ábráról az
is látszik, hogy egyenletünk megoldása nem lehet pozitív mennyiség, különben az
a hosszúságú átfogó nem lenne nagyobb a másik, a 2x+a hosszúságú
befogónál. Ezt persze ránézéssel is tudhatjuk: az ![]() alakú egyenletnek
pozitív megoldása nem lehet, hiszen ilyen esetben a kiindulási egyenletünk bal
oldala pozitív lesz, a jobb oldalán viszont negatív szám áll. Ha a 2x+a
hosszúságú befogót (levonó átkörzéssel) levonjuk az a hosszúságú
átfogóból, akkor egy 2x hosszúságú „negatív” távolságot kapunk, amelynek
felezésével megkapjuk egyenletünk első (negatív előjelű) megoldását, az x1-et.
Egyenletünk másik megoldását az átfogó újbóli elmetszésével (az M pontnál)
állíthatjuk elő. Ha a 2x+a hosszúságú befogót (a negatív előjelű
befogót, hozzáfűző átkörzéssel) az a hosszúságú átfogóhoz adjuk (-(2x+a) + a = -2x), akkor egy 2x hosszúságú
„negatív” távolságot kapunk (2x º MN), amelynek felezésével megkapjuk
az
alakú egyenletnek
pozitív megoldása nem lehet, hiszen ilyen esetben a kiindulási egyenletünk bal
oldala pozitív lesz, a jobb oldalán viszont negatív szám áll. Ha a 2x+a
hosszúságú befogót (levonó átkörzéssel) levonjuk az a hosszúságú
átfogóból, akkor egy 2x hosszúságú „negatív” távolságot kapunk, amelynek
felezésével megkapjuk egyenletünk első (negatív előjelű) megoldását, az x1-et.
Egyenletünk másik megoldását az átfogó újbóli elmetszésével (az M pontnál)
állíthatjuk elő. Ha a 2x+a hosszúságú befogót (a negatív előjelű
befogót, hozzáfűző átkörzéssel) az a hosszúságú átfogóhoz adjuk (-(2x+a) + a = -2x), akkor egy 2x hosszúságú
„negatív” távolságot kapunk (2x º MN), amelynek felezésével megkapjuk
az ![]() alakú egyenlet másik,
a negatív előjelű megoldását, az x2-őt (ezt a hozzáfűző
„trükköt” a görögök nem csinálták!).
alakú egyenlet másik,
a negatív előjelű megoldását, az x2-őt (ezt a hozzáfűző
„trükköt” a görögök nem csinálták!).
Az ![]() alakú kifejezés -
alakú kifejezés -
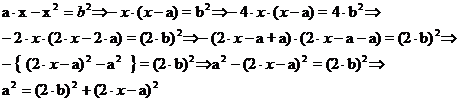
- átalakításaival azt kaptuk, hogy az a, a
2b és a 2x-a mennyiségek
között pitagorászi összefüggés áll fenn; vagyis a felsorolt mennyiségek egy
derékszögű háromszög oldalai (lásd a 3. ábrát!). Itt a szerkesztéssel kapott 2x-a hosszúságú befogó "tartalmazza" a keresett x
távolságot. A gyökvonás kétértékűsége miatt a 2x-a mennyiséget egyszer pozitívnak, majd negatívnak kell
gondolnunk, így hosszát 2x-a-nak illetve -(2x-a)-nak kell venni.
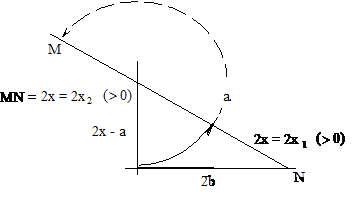
3. ábra. Az ![]() alakú (elliptikus)
egyenlet geometriai megoldásának vázlata; az ilyen alakú egyenleteknek negatív
gyöke nem lehet. Az a és 2b távolságok ismeretében, a > 2b esetén a derékszögű háromszög megszerkeszthető, így az
egyenlet gyökeit a bejelölt 2x1 és 2x2
távolságok megfelezésével kapjuk meg
alakú (elliptikus)
egyenlet geometriai megoldásának vázlata; az ilyen alakú egyenleteknek negatív
gyöke nem lehet. Az a és 2b távolságok ismeretében, a > 2b esetén a derékszögű háromszög megszerkeszthető, így az
egyenlet gyökeit a bejelölt 2x1 és 2x2
távolságok megfelezésével kapjuk meg
A 3. ábráról azonnal látszik a
derékszögű háromszög megszerkeszthetőségének, az ![]() alakú egyenlet
megoldhatóságának a geometriai feltétele: a > 2b; az a átfogónak nagyobbnak kell
lennie bármelyik befogónál, így a 2b-nél is és a 2x-a-nál is. A 2x-a befogó (a-2x, vagy 2x-a) hosszának a átfogóra történő
(kétszeri) átkörzésével, levonásával és hozzáadásával (a második metszéspont az
M pontnál (ezt a hozzáfűző „trükköt” a görögök nem csinálták)), előállítható
egyenletünk mindkét pozitív gyöke: az x1, és az x2
megoldások kétszerese (lásd a 3. ábrát!); ezek megfelezésével kapjuk meg a
keresett gyököket. A 3. ábráról az is látszik, hogy egyenletünk x
megoldása nem lehet negatív mennyiség, különben az a hosszúságú átfogó
nem lenne nagyobb a 2x-a hosszúságú befogónál. Ezt persze ránézéssel is
tudhatjuk, hiszen az
alakú egyenlet
megoldhatóságának a geometriai feltétele: a > 2b; az a átfogónak nagyobbnak kell
lennie bármelyik befogónál, így a 2b-nél is és a 2x-a-nál is. A 2x-a befogó (a-2x, vagy 2x-a) hosszának a átfogóra történő
(kétszeri) átkörzésével, levonásával és hozzáadásával (a második metszéspont az
M pontnál (ezt a hozzáfűző „trükköt” a görögök nem csinálták)), előállítható
egyenletünk mindkét pozitív gyöke: az x1, és az x2
megoldások kétszerese (lásd a 3. ábrát!); ezek megfelezésével kapjuk meg a
keresett gyököket. A 3. ábráról az is látszik, hogy egyenletünk x
megoldása nem lehet negatív mennyiség, különben az a hosszúságú átfogó
nem lenne nagyobb a 2x-a hosszúságú befogónál. Ezt persze ránézéssel is
tudhatjuk, hiszen az ![]() alakú egyenletnek nem
lehet negatív előjelű megoldása; negatív x esetén
ellentmondáshoz jutunk: az egyenlet bal oldalán negatív, jobb oldalán viszont
pozitív szám lesz. Itt is érdemes megemlíteni, hogy egyenletünk megoldhatóságának
feltételét geometriai tényekből és nem algebrai megfontolásokból kaptuk meg (az
alakú egyenletnek nem
lehet negatív előjelű megoldása; negatív x esetén
ellentmondáshoz jutunk: az egyenlet bal oldalán negatív, jobb oldalán viszont
pozitív szám lesz. Itt is érdemes megemlíteni, hogy egyenletünk megoldhatóságának
feltételét geometriai tényekből és nem algebrai megfontolásokból kaptuk meg (az
![]() alakú egyenlet
diszkriminánsa a2 -
4b2, ezért az algebrai megoldhatóság feltétele: a > 2b).
alakú egyenlet
diszkriminánsa a2 -
4b2, ezért az algebrai megoldhatóság feltétele: a > 2b).
Az ![]() alakú kifejezés -
alakú kifejezés -
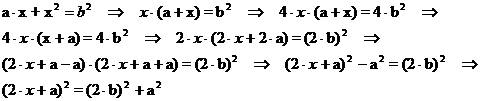
- átalakításaival azt kaptuk, hogy az a, a
2b és a 2x + a
mennyiségek között pitagorászi összefüggés áll fenn; vagyis a felsorolt mennyiségek egy
derékszögű háromszög oldalai (lásd a 4. ábrát!). Itt a szerkesztéssel kapott 2x+a
hosszúságú átfogó "tartalmazza" a keresett x távolságot. A gyökvonás
kétértékűsége miatt a 2x+a mennyiséget egyszer pozitívnak, majd
negatívnak kell gondolnunk, így hosszát 2x+a-nak illetve -(2x+a)-nak kell venni.
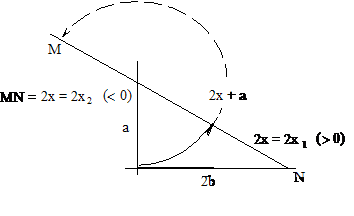
4. ábra. Az ![]() alakú (hiperbolikus)
egyenlet geometriai megoldásának vázlata; az a és 2b távolságok
ismeretében a derékszögű háromszög megszerkeszthető, így az egyenlet gyökeit a
bejelölt 2x1 és 2x2 távolságok
megfelezésével kapjuk meg
alakú (hiperbolikus)
egyenlet geometriai megoldásának vázlata; az a és 2b távolságok
ismeretében a derékszögű háromszög megszerkeszthető, így az egyenlet gyökeit a
bejelölt 2x1 és 2x2 távolságok
megfelezésével kapjuk meg
A 4. ábráról látszik, hogy a
derékszögű háromszög megszerkeszthetőségének, így az ![]() egyenlet
megoldhatóságának nincsen geometriai feltétele; de ennek így is kell lennie, hiszen
az ilyen alakú egyenletek diszkriminánsa, az a2 + 4b2 mindig
pozitív. Ilyen esetekben két gyököt várunk: az a befogó 2x+a átfogóra
történő kétszeri átkörzésével, levonással, illetve hozzáadással (a második
metszéspont az M pontnál (ezt a hozzáfűző „trükköt” a görögök nem csinálták)),
előállítható egyenletünk mindkét gyöke: a pozitív x1, és a
negatív x2 megoldások kétszerese (lásd a 4. ábrát!); ezek megfelezésével kapjuk meg a
keresett gyököket.
egyenlet
megoldhatóságának nincsen geometriai feltétele; de ennek így is kell lennie, hiszen
az ilyen alakú egyenletek diszkriminánsa, az a2 + 4b2 mindig
pozitív. Ilyen esetekben két gyököt várunk: az a befogó 2x+a átfogóra
történő kétszeri átkörzésével, levonással, illetve hozzáadással (a második
metszéspont az M pontnál (ezt a hozzáfűző „trükköt” a görögök nem csinálták)),
előállítható egyenletünk mindkét gyöke: a pozitív x1, és a
negatív x2 megoldások kétszerese (lásd a 4. ábrát!); ezek megfelezésével kapjuk meg a
keresett gyököket.
A bemutatott módszer
általánosításaként érdemes végiggondolni még egyszer a bemutatottakat úgy is,
hogy az említett kiindulási egyenletek átalakításainál nem 4-gyel, hanem
valamilyen másik négyzetszámmal szorozzuk meg az egyenleteket.
1. táblázat.
|
Az egyenlet típusa |
A megoldhatóság geometriai feltétele és az algebrai feltétel |
Gyökök száma és előjele |
|
|
Nincs geometriai feltétel. Az a2 + 4b2
diszkrimináns mindig pozitív. |
Két gyök van: + és - |
|
|
a > 2b. A diszkrimináns: a2 -
4b2 > 0. |
Két negatív gyök van, pozitív gyök nem is lehet. |
|
|
a > 2b. A diszkrimináns: a2 -
4b2 > 0. |
Két pozitív gyök van, negatív gyök nem is lehet. |
|
|
Nincs geometriai feltétel. Az a2 + 4b2
diszkrimináns mindig pozitív. |
Két gyök van: + és - |
A másodfokú egyenletek körzővel és
vonalzóval történő megoldása nem új keletű dolog. Mindenesetre nagyon érdekes,
hogy az általam leírt módon az egyenletek mindkét gyökét meg lehet
szerkeszteni. Szerintem az is nagyon meglepő, hogy az egyenletek megoldhatósága
milyen egyszerű geometriai feltételekből adódik; de a legmeglepőbb dolog az, hogy
milyen szép szimmetriákat illetve hasonlóságokat lehet felismerni az egyes
megoldások között (lásd, pl. a táblázatot!). A bemutatott módszer kapcsán bízom
abban, hogy az itt leírtak sok örömet okoznak tanárnak-diáknak; és abban is bízom, hogy a sumptoma-k jobb oldalára bevezetett – b2, illetve a
negatív megoldások megtalálása (és főleg elfogadása) miatt „szigorú görög
mestereink nem forognak a sírjukban”.
Dolgozatomat -
köszönet és hálaként -
egykori matematika tanáraim emlékének ajánlom
Számtan és
mértan tanáraim a Solymári Általános Iskolában: Horváthné, Erzsébet tanító néni; Szentpéteri Endre tanító bácsi; Temesi Mátyás tanító bácsi; Gróbné Bacsányi Gyöngyi tanárnő,
általános iskolai tanár; Csöndes József tanár úr, általános
iskolai tanár.
Matematika
tanárom az Esztergomi Szent István Gimnáziumban: Marton Kálmán tanár úr,
középiskolai matematika tanár.
A JATE Bolyai
Intézetében matematikára oktató tanáraim (és akkori beosztásuk); az Ő aláírásuk szerepel az
indexemben: Dr. Rédey László egyetemi tanár, Dr. Leindler László egyetemi
tanár, Dr. Tandori Károly egyetemi tanár, Dr. Soós Gyula egyetemi tanár, Dr.
Fodor Géza egyetemi tanár, Dr. Szőkefalvi-Nagy Béla egyetemi tanár, Dr. Kalmár
László egyetemi tanár, Dr. Csákány Béla egyetemi docens, Dr. Pintér Lajos
egyetemi docens, Dr. Muszka Dániel tudományos
főmunkatárs, Dr. Gehér László egyetemi adjunktus, Dr. Megyesi László
egyetemi adjunktus, Dr. Peák István egyetemi adjunktus, Dr. Berkes Jenő
egyetemi adjunktus, Dr. Csúriné dr. Paár Piroska egyetemi adjunktus, Dr.
Szenthe János egyetemi adjunktus, Dr. Hatvani László egyetemi tanársegéd, Dr.
Durszt Endre egyetemi tanársegéd, Dr. Szűcs József egyetemi tanársegéd, Dr.
Pollák György tudományos munkatárs, Dr. Pávó Imre tudományos munkatárs, Dr.
Salánkiné dr. Gulácsi Sára tudományos munkatárs, Dr. Hunya Péter tudományos
munkatárs, Dr. Csúri József középiskolai tanár és Dr. Bakos László középiskolai
tanár.
Feladatok
1. Oldja meg
geometriailag a 20·x – x2 =
64 (elliptikus) egyenletet! (x1
= 4 és x2 = 16).
2. Oldja meg
geometriailag a 12·x + x2 =
64 (hiperbolikus) egyenletet! (x1
= 4 és x2 = –16).
5. Oldja meg
geometriailag a 16·x = 64 (parabolikus) egyenletet! (x = 4).
6. Oldja meg
geometriailag Brahmagupta híres, a 10×x + x2 = 39 alakban megadott (hiperbolikus) egyenletét
is! (x1 = 3 és x2 = -13; Brahmagupta módszerével csak az x1
= 3 gyököt lehet megtalálni).
Irodalom
[1] Ringler András: Másodfokú egyenletek
geometriai megoldása, 2002, POLYGON, Szeged, XI. évfolyam, 2. szám, 60-65.
[2] Ringler András: A ![]() , 2003, A Matematika Tanítása, Mozaik Oktatási Stúdió,
Szeged, XI. évfolyam, 2. szám, 17-23.
, 2003, A Matematika Tanítása, Mozaik Oktatási Stúdió,
Szeged, XI. évfolyam, 2. szám, 17-23.
[3] Filep László: A tudományok
királynője, 1997, TYPOTEX Kft. - Budapest, Bessenyei Kiadó - Nyíregyháza, ISBN
963 7546 83 9.
[4] Ringler András: Fizikai szemléletünk
gyökerei, 2001, A Fizika Tanítása, Mozaik Oktatási Stúdió, Szeged, IX.
évfolyam, 4. szám, 4-10.
[5] Simonyi Károly: A fizika
kultúrtörténete, 1998, Akadémiai Kiadó, ISBN 963 05 7651 2.
[6]
Ringler András: Mi köze van a szabályos háromszögnek a szabályos ötszöghöz,
2004, A Matematika Tanítása, Mozaik Oktatási Stúdió, Szeged, XII. évfolyam, 4.
szám, 3-7.
Szeged, 2006.
március 14. Dr. habil.
Ringler András Ph.D.