Ringler András és Füvesi István

A szabályos ötszög szerkesztése egyenlő oldalú háromszögből

Kulcsszavak: szabályos pentagon, szabályos ötszög szerkesztése, pitagóreusok szimbóluma.

Az előadó azt mutatja meg, hogy kiindulva egy szabályos háromszögből, olyan adatokhoz jutunk, amelyek segítségével a pitagóreusok titkos szimbóluma, a szabályos ötszög, körzővel és vonalzóval, könnyedén megszerkeszthető.

A derékszögű háromszögekkel kapcsolatosan gyakran használt magasság-tételt szinte mindenki ismeri. Azt azonban már kevesebben tudják, hogy ez a tétel egy általánosabb tételnek, a szelőszakaszok-tételének csupán egy speciális esete. Könnyű megmutatni, hogy ezen állítások hátterében a kör tulajdonsága, „a kör egyenlete áll”.

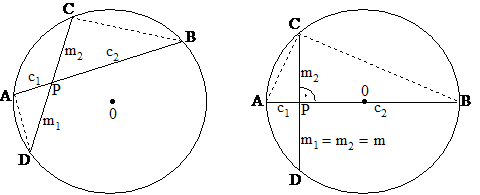
1. ábra. Egy kör két húrja a P pontban metssze egymást (az ábra bal oldali része). Speciális esetként, az egyik húr lehet a kör átmérője, a másik húr (a CD húr) pedig legyen merőleges az AB átmérőre

Egy körben két egymást metsző AB és CD szelőszakasz, két húr közös pontja legyen P. Az 1. ábra bal oldali részét nézve könnyű belátni, hogy az ADP D hasonló a PBC D-höz, Þ , Þ ; és ez minden, a P ponton átmenő szelőszakaszra igaz. Ha az AB szelőszakasz (speciális esetként) átmegy a kör középpontján, (vagyis, ha az AB húr éppen átmérő, lásd az 1. ábra jobb oldali részét), és a CD szelőszakasz merőleges az AB szelőszakaszra, akkor az ABC D derékszögű háromszög lesz, ekkor miatt . E kifejezés éppen a magasság-tétel, amely szerint a derékszögű háromszög átfogójához tartozó m magasság mértani közepe az átfogó megfelelő két részének, a c₁ és a c₂ távolságoknak.

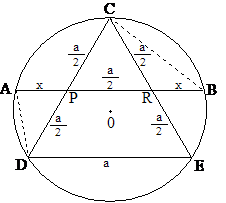
2. ábra. Az a oldalú szabályos háromszög köré rajzolt körrel kapott ábra érdekessége, hogy a kör berajzolásával adódó x távolság és az távolság aranyarányban vannak egymással. E két távolsággal a szabályos ötszög, például a szabályos ötágú csillag könnyedén megszerkeszthető (lásd a 3. ábra jobb oldali részét!)

A szelőszakaszok-tételének ismerete hasznos dolog, hiszen segítségével válaszolhatunk a következő kérdésre: mi köze van egy szabályos háromszögnek a szabályos ötszöghöz? E kérdés megválaszolásához egy a oldalú szabályos háromszög köré rajzolt körön, az a oldalú, DEC háromszög CD és CE oldalainak P és R felezőpontjait összekötő húr körrel közös pontjait jelölje A és B, (lásd a 2. ábrát!). Mivel AP = RB = x, PB = és CP = PD = , ezért az AB és CD húrok megfelelő részeivel felírva az előbb említett szelőszakaszok tételét, a következő kifejezéshez jutunk:

. (*)

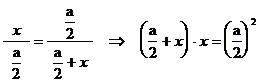Ez az összefüggés azt „mondja”, hogy az távolság mértani közepe az és az x távolságoknak. (*) jobb oldalának rendezésével az hiperbolikus szümptómához (egyenlethez) jutunk, amelynek algebrai megoldásával és adódik. Ez a tény roppant érdekes, hiszen arról tájékoztat, hogy az x és az távolságok aranyarányban vannak egymással; az ilyen tulajdonságú távolságokat aranyszomszédoknak nevezzük. Vegyük észre, hogy (*) bal oldalán a szabályos ötágú csillagból is jól ismert arany-arány látható. Tudjuk, hogy a szabályos ötszög, körzővel és vonalzóval történő megszerkesztéséhez arany-arányban lévő távolságokra van szükség; hiszen ezek segítségével, például a 72^o-os szög, a szabályos ötszög középponti szöge megszerkeszthető. A görögök idején az alakú, ún. hiperbolikus szümptómákat (egyenleteket) még nem algebrailag, hanem geometriailag, tehát körzővel és vonalzóval oldották meg; de mivel a görögök a negatív számokat nem ismerték, ezért a negatív megoldás nem is érdekelhette őket. A görögök mára már majdnem elfelejtett geometriai módszere nagyon érdekes, felidézésével, a megoldó képlet használata, tehát algebrai ismeretek nélkül jöhetünk rá, hogy mi köze a szabályos háromszögnek a szabályos ötszöghöz: a 2. ábrán olyan adatok vannak, amelyek segítségével a szabályos ötszög, például a szabályos ötágú csillag megszerkeszthető.

Az alakban adott hiperbolikus szümptóma geometriai megoldása önmagában is érdekes tanárnak-diáknak egyaránt ([1], [2], [3] és [4]). Az ilyen szümptómák geometriai megoldásával adódó x és az távolságok aranyarányban vannak egymással, ezért e távolságok ismeretében a szabályos ötszög, például a pitagóreusok titkos szimbóluma, a szabályos ötágú csillag, körzővel és vonalzóval megszerkeszthető.

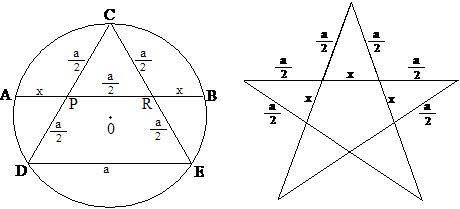
3. ábra. Az ábra bal oldali részén előállított x és távolságok segítségével a szabályos ötágú csillag, „lépésről-lépésre”, körzővel és vonalzóval megszerkeszthető: "az ábra jobb oldali része önmagáért beszél"

Ha az kifejezésben az távolság lenne az ismeretlen és az távolság lenne az előre ismert távolság, akkor a kifejezésből adódó alakú elliptikus szümptómát kellene körzővel és vonalzóval megoldani. Az ilyen alakú egyenleteket, a alakú tag „fellépése” miatt a görögök nem tudták megoldani, pedig az ilyen alakú elliptikus szümptómáknak mindig létezik egy pozitív és egy negatív megoldása ([1], [3] és [4]).

A másodfokú egyenletek körzővel és vonalzóval történő megoldása megtekinthető on-line, vagy a tanári munka segítése céljából szabadon letölthető a MOZAIK honlapjáról:

www.mozaik.info.hu/homepage/mozaportal/matematika.php

A program népszerűségét mi sem bizonyítja jobban, hogy a letöltések száma, már 8000 fölött van.

Összefoglalás

Egy a oldalú szabályos háromszögből, a 2. vagy a 3. ábrán előállított x és távolságok segítségével a pitagóreusok titkos szimbóluma, a szabályos ötszög, a szabályos ötágú csillag, körzővel és vonalzóval, „lépésről-lépésre”, könnyedén megszerkeszthető (lásd a 3. ábra jobb oldali részét, az ábra önmagáért beszél!).

Irodalom

[1] RINGLER A., 2003, Gondolkozzunk görögül, A Matematika Tanítása, Mozaik, XI. évfolyam, 5. szám, 3-8.

[2] RINGLER A., 2004, Mi köze van a szabályos háromszögnek a szabályos ötszöghöz? A Matematika Tanítása, Mozaik, XII. évfolyam, 4. szám, 3-7.

[3] RINGLER A., 2006, Másodfokú egyenletek görög megoldása és a módszer általánosítása, A Matematika Tanítása, Mozaik, XIV. évfolyam, 4. szám, 8-14.

[4] www.mozaik.info.hu/homepage/mozaportal/matematika.php