Ringler András

Apollóniosz szümptómái

A matematikai gondolkodás fejlődésének bemutatása nagyon fontos és roppant érdekes feladat. Ennek ellenére kevés időt áldozunk erre az iskolai munka során, pedig a görögök matematikája mindenkit csodálatba ejt. Az irracionális számok felfedezése kapcsán a görög matematikában jelentkezett válság megoldására az irracionalitás gondolatát egyszerűen áttolták a geometriába: irracionális számok nincsenek, csupán irracionális mennyiségek, pl. szakaszok. Ilyen előzmények után érthető, hogy a görög geometria hatalmas fejlődésnek indult. Szinte minden matematikai problémát geometriai módszerekkel akartak megoldani. Éppen ezért nem kell csodálkozni azon, hogy a másodfokú egyenleteket is geometriailag, tehát körzővel és vonalzóval oldották meg ([1], [2], [3]).

A másodfokú egyenletek megoldásához az elliptikus-, a hiperbolikus- és a parabolikus illesztések gondolatát Euklidesz vetette fel, és használta másodfokú egyenletek megoldására. Az ellipszis, a hiperbola és a parabola fogalmának geometriába történő bevezetése azonban a pergai Apollóniosz (-262?, -190?) nevéhez fűződik. Az ellipszis "egyenletének" apollónioszi levezetésével Filep László könyvében ([1]) találkoztam és mondhatom roppant tanulságos volt, a több mint 2000 éves gondolatokkal való ismerkedés. A dolog megértése után kíváncsi lettem arra, hogy hasonló módon, vajon hogyan lehetne levezetni a hiperbola és a parabola egyenletét is. Miután rájöttem erre, és a levezetéshez szükséges gondolatmenetet érdekesnek illetve tanulságosnak tartom, ezért ezeket kellő előkészítés után közreadom. Dolgozatommal, a több mint 2000 éves ismeretek felidézésével a kúpszeletek specialistája, a "pergai óriás" gondolatai előtt kívánok tisztelegni. A kúpszeletek felismerése Menaikhmosz, a konhoisz görbe felfedezőjének a nevéhez fűződik; aki -300 körül - a kocka térfogatának kétszerezése kapcsán - az a oldalú négyzet területének kétszerezésére "felállított" a : x = x : 2a aránnyal analógiában kísérelte meg az a oldalú kocka térfogatánál kétszer nagyobb térfogatú kocka oldalhosszának az előállítását ([4]). Arra gondolt, hogy az ezt biztosító x távolságot a hippokráteszi a : x = x : y = y : 2a arányokból lehet meghatározni: mai szóhasználattal az a : x = x : y összefüggésből az (parabola), az a : x = y : 2a összefüggésből pedig az (hiperbola) kifejezésekhez jutva, ezek metszéspontjaként adódik. Ez az x távolság éppen az a oldalú kocka térfogatánál kétszer nagyobb térfogatú kocka oldalának a hossza. -

Az apollónioszi ötletek újragondolásához idézzük fel a derékszögű háromszögekre gyakran használt magasságtételt. A tétel szerint a derékszögű háromszög átfogójához tartozó magasság mértani közepe az átfogó megfelelő két részének. Az 1. ábra jobb oldali részén látható rajz jelöléseivel: . Ezt az egyenlőséget a görögök így értelmezték: a DO és az OE szakaszokból készített téglalap (DO×OE) területe megegyezik az OP oldalú négyzet (OP²) területével. A "régi geométerek" ezzel a feltétellel definiálták a kör egyenletét, hiszen a kör minden P pontjának ki kell elégítenie az említett kifejezést, az Ő szóhasználatukkal a kör sumptoma-ját. A magasságtételről könnyű megmutatni, hogy valójában a kör egyenletét "takarja". Ennek igazolására vezessük be a következő jelöléseket: OP = y, DO = x, OE = 2×r - x, ahol r a kör sugarát jelöli. Írjuk ezeket a magasságtétel fenti alakjába:

y² = x×(2×r - x) Þ y² = 2×r×x - x² = 2×r×x - x² + r² - r² Þ (x - r)² + y² = r².

Ezzel egy r sugarú, (r,0) középpontú kör egyenletéhez jutottunk. A magasság-tételben megfogalmazottakat ezért nyugodtan nevezhetjük a kör sumptoma-jának, modern szóval a kör egyenletének. Ezek után már könnyen juthatunk az ellipszis, a hiperbola, és a parabola sumptoma-jához is: ehhez nézzük az 1. ábrát és olvassuk el a rá vonatkozó szöveget; ezután folytassuk a 2. ábrával és a hozzá tartozó magyarázó szöveggel; majd a 3. ábrával ugyanígy.

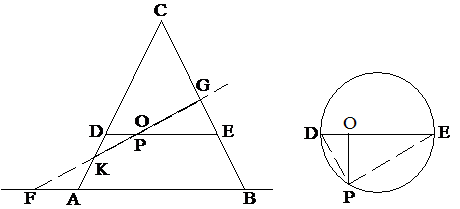
1. ábra. A vízszintes síkon álló egyenes kúp oldalnézetből - a rajz síkjában lévő metszeten - háromszögnek látszik. Az ABC pontokkal jellemzett kúpot (a rajz síkjára merőlegesen álló) alkalmasan elmetsző sík és a kúp palástja közös része ellipszist ad, amelyet - oldalnézetben - a GK "szakasz" szemléltet

A vízszintes síkon álló ABC egyenes kúpot egy megfelelő, a rajzon az FG vonallal szemléltetett ferde síkkal elmetszve a kúp palástja és a ferde metszősík közös része ellipszist "ad". A rajz síkjára merőlegesen álló metszősík a kúpot (oldalnézetben) a KG vonal mentén metszi el (lásd az 1. ábrát!). Metsszük el a kúpot valahol a K és a G pontok között egy vízszintes síkkal is. A kúpon keletkezett kör alakú metszésvonalat oldalnézetben a DE vonal jelzi, fölül-nézetben pedig az ábra jobb oldala mutatja. Az egymást metsző ellipszis és e kör egyik közös pontját jelölje P. A kör átmérőjén lévő O pont a kör kerületi P pontja átmérőre vetítésével adódik; az OP távolság ezért a bejelölt DPE derékszögű háromszög átfogójának a magassága. Mivel a P pont rajta van a körön is és az ellipszisen is, ezért a P pontnak ki kell elégítenie a kör sumptoma-ját, mai szóhasználattal a kör egyenletét. Ha a kúpot metsző vízszintes sík önmagával párhuzamosan a K és a G pontok között függőlegesen elmozdul, akkor a P pont mindig másik vízszintes helyzetű körre kerül, de közben "végigtapogatja" a rögzített helyzetű ellipszis pontjait, ezzel "kirajzolja" az ellipszis sumptoma-ját. A vízszintes helyzetű metszősík G ponttól lefelé történő süllyedését pl. a GO távolság növekedésével jellemezhetjük. Ezt a távolságot, mai szóhasználattal x koordinátának, az OP távolságot pedig y koordinátának nevezzük. Az ellipszis paramétereit nyilván a kúp adatai és a ferdén metsző sík kúphoz való viszonya határozza meg.

Az 1. ábrán - oldalnézetben - látszik, hogy az ODK D hasonló az FAK D-höz, és az OEG D hasonló az FBG D-höz, ezért a megfelelő oldalak arányának felírásával

és

adódik. Az ezekből kiszámolt

és

kifejezéseket beírva a kör egyenletébe (sumptoma-jába), adódik az

kifejezés. Ebből az

jelölések bevezetésével megkapjuk az ellipszis

alakú egyenletét. Az ellipszis szó a görögök mindent átható geometriai szemléletéből adódik. Ők a kapott egyenletet (sumptoma-t) így értelmezték: a p hosszúságú szakaszhoz olyan x magasságú téglalapot kell illeszteni, amelynek p×x területéből a×x² területet elhagyva egy y oldalú négyzet (y²) területét kapjuk. A görögök ezt az a×x² területhiánnyal történő illesztést elliptikus illesztésnek, a szümptóma által kijelölt görbét pedig ellipszisnek nevezték el: az elleipsis szó tehát a hiányra utal.

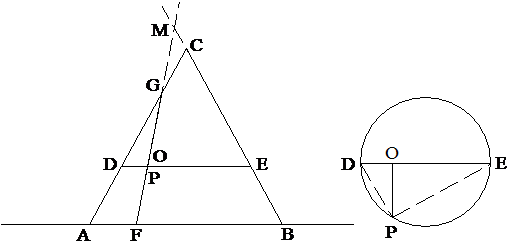
2. ábra. A vízszintes síkon álló egyenes kúp oldalnézetből - a rajz síkjában lévő metszeten - háromszögnek látszik. Az ABC pontokkal jellemzett kúpot (a rajz síkjára merőlegesen álló) alkalmasan elmetsző sík és a kúp palástja közös része hiperbolát ad, amelyet - oldalnézetben - a GF "szakasz" szemléltet

A vízszintes síkon álló ABC egyenes kúpot egy megfelelő, a rajzon az FM vonallal szemléltetett ferde síkkal elmetszve a kúp palástja és a ferde metszősík közös része hiperbolát "ad". A rajz síkjára merőlegesen álló metszősík a kúpot (oldalnézetben) a GF vonal mentén metszi el (lásd az 2. ábrát!). Metsszük el a kúpot valahol az F és a G pontok között egy vízszintes síkkal is. A kúpon keletkezett kör alakú metszésvonalat oldalnézetben a DE vonal jelzi, fölül-nézetben pedig az ábra jobb oldala mutatja. Az egymást metsző hiperbola és e kör egyik közös pontját jelölje P. A kör átmérőjén lévő O pont a kör kerületi P pontja átmérőre vetítésével adódik; az OP távolság ezért a bejelölt DPE derékszögű háromszög átfogójának a magassága. Mivel a P pont rajta van a körön is és a hiperbolán is, ezért a P pontnak ki kell elégítenie a kör sumptoma-ját, mai szóhasználattal a kör egyenletét. Ha a kúpot metsző vízszintes sík önmagával párhuzamosan a G és az F pontok között függőlegesen elmozdul, akkor a P pont mindig másik vízszintes helyzetű körre kerül, de közben "végigtapogatja" a rögzített helyzetű hiperbola pontjait, ezzel "kirajzolja" a hiperbola sumptoma-ját. A vízszintes helyzetű metszősík G ponttól lefelé történő süllyedését pl. a GO távolság növekedésével jellemezhetjük. Ezt a távolságot, mai szóhasználattal x koordinátának, az OP távolságot pedig y koordinátának nevezzük. A hiperbola paramétereit nyilván a kúp adatai és a ferdén metsző sík kúphoz való viszonya határozza meg.

A 2. ábrán - oldalnézetben - látszik, hogy a DOG D hasonló az AFG D-höz, és az OEM D hasonló az FBM D-höz, ezért a megfelelő oldalak arányának felírásával

és

adódik. Az ezekből kiszámolt

és

kifejezéseket beírva a kör egyenletébe (sumptoma-jába), adódik az

kifejezés. Ebből az

jelölések bevezetésével megkapjuk a hiperbola

alakú egyenletét. A hiperbola szó a görögök mindent átható geometriai szemléletéből adódik. Ők a kapott egyenletet (sumptoma-t) így értelmezték: a p hosszúságú szakaszhoz olyan x magasságú téglalapot kell illeszteni, amelynek p×x területéhez a×x² területet adva egy y oldalú négyzet (y²) területét kapjuk. A görögök ezt az a×x² területtöbblettel történő illesztést hiperbolikus illesztésnek, a szümptóma által kijelölt görbét pedig hiperbolának nevezték el: a hiperbole szó tehát a többletre utal.

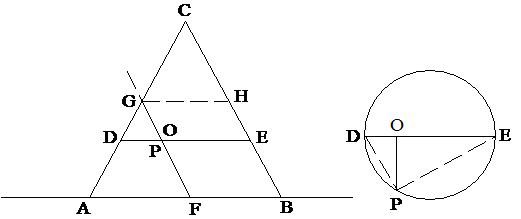
3. ábra. A vízszintes síkon álló egyenes kúp oldalnézetből - a rajz síkjában lévő metszeten - háromszögnek látszik. Az ABC pontokkal jellemzett kúpot (a rajz síkjára merőlegesen álló) alkalmasan elmetsző sík és a kúp palástja közös része parabolát ad, amelyet - oldalnézetben - a GF "szakasz" szemléltet

A vízszintes síkon álló ABC egyenes kúpot egy megfelelő, a rajzon az FG vonallal szemléltetett ferde síkkal elmetszve a kúp palástja és a ferde metszősík közös része parabolát "ad". A rajz síkjára merőlegesen álló metszősík a kúpot (oldalnézetben) a GF vonal mentén metszi el (GF párhuzamos CB-vel, (lásd az 3. ábrát!).). Metsszük el a kúpot valahol a G és az F pontok között egy vízszintes síkkal. A kúpon keletkezett kör alakú metszésvonalat oldalnézetben a DE vonal jelzi, fölül-nézetben pedig az ábra jobb oldala mutatja. Az egymást metsző parabola és e kör egyik közös pontját jelölje P. A kör átmérőjén lévő O pont a kör kerületi P pontja átmérőre vetítésével adódik; az OP távolság ezért a bejelölt DPE derékszögű háromszög átfogójának a magassága. Mivel ez a P pont rajta van a körön is és a parabolán is, ezért a P pontnak ki kell elégítenie a kör sumptoma-ját, mai szóhasználattal a kör egyenletét. Ha a kúpot metsző vízszintes sík önmagával párhuzamosan a G és az F pontok között függőlegesen elmozdul, akkor a P pont mindig másik vízszintes helyzetű körre kerül, de közben "végigtapogatja" a rögzített helyzetű parabola pontjait, ezzel "kirajzolja" a parabola sumptoma-ját. A vízszintes helyzetű metszősík G ponttól lefelé történő süllyedését pl. a GO távolság növekedésével jellemezhetjük. Ezt a távolságot, mai szóhasználattal x koordinátának, az OP távolságot pedig y koordinátának nevezzük. A parabola paramétereit nyilván a kúp adatai és a ferdén metsző sík kúphoz való viszonya határozza meg. A rajzon látható H segédpontot a DE szakasszal párhuzamosan rajzolt, a G ponton átmenő egyenes segítségével kapjuk meg; ezért a H pontra teljesül, hogy GH = OE.

A 3. ábrán - oldalnézetben - látszik, hogy a DOG D hasonló az AFG D-höz, és a GHC D hasonló az ABC D-höz (is), ezért a megfelelő oldalak arányának felírásával

és

adódik. Az ezekből kiszámolt

és

kifejezéseket beírva a kör egyenletébe (sumptoma-jába), adódik az

kifejezés. Ebből az

jelölések bevezetésével megkapjuk a parabola

alakú egyenletét. A parabola szó a görögök mindent átható geometriai szemléletéből adódik. Ők a kapott egyenletet (sumptoma-t) így értelmezték: a p hosszúságú szakaszhoz olyan x magasságú téglalapot kell illeszteni, amelynek p×x területéhez nulla területet adva (illetve levonva) egy y oldalú négyzet (y²) területét kapjuk. A görögök ezt a sem terület-többlettel, sem terület-hiánnyal, vagyis megegyezésben (nulla területtel) történő illesztést parabolikus illesztésnek, a szümptóma által kijelölt görbét pedig parabolának nevezték el: a parabole szó tehát; a megegyezésben, vagyis többlet és hiány nélküli egybevetésre utal.

Az 1000 évig virágzó görög matematika a hellenizmus korában érte el fénykorát. Ekkor alkotott Euklidesz, Menaikhmosz, Arisztarkhosz, Archimédesz, Eratosztenész és a kortársak által még Euklidesznél is nagyobb geométernek tartott Apollóniosz is. Annak ellenére, hogy a geometriai bizonyítások nagyon megnehezítették a matematika fejlődését, Apollóniosz bizonyításait még ma is a geometria gyöngyszemeinek tekintjük. Bár a kúpszeletek elméletével mások is foglalkoztak, az egységes tárgyalás a "pergai óriástól", a "megas geometrhs"-től származik.

Irodalom

[1] Filep László: A tudományok királynője, 1997, TYPOTEX Kft. - Budapest, Bessenyei Kiadó - Nyíregyháza, ISBN 963 7546 83 9.

[2] Ringler András: Másodfokú egyenletek geometriai megoldása, POLYGON, 2002, XI. kötet 2. szám, 60-65.

[3] Ringler András, Gondolkozzunk "görögül", 2003, A Matematika Tanítása, Mozaik Oktatási Stúdió, XI. évfolyam, 5. szám, 3-8.

[4] Lévárdi László és Sain Márton: Matematikatörténeti feladatok, 1982, Tankönyvkiadó, Budapest.