A koszinusz-tétel "előáll" a Tabit-tételből
A
régi mesterek eredményeinek felidézése számos intellektuális öröm forrása. A
már-már elfelejtett ismeretek tanulmányozása során gyakran találkozhatunk
félbeszakadtnak tűnő gondolatokkal, amelyek továbbfűzésével még ma is érdekes
eredményekhez juthatunk [1].
Szerencsés az ember, ha így talál meg valamit. Így jártam én is, amikor
elolvastam Lévárdi és Sain "Matematikatörténeti feladatok" című
munkájában a »1100
éves Tabit-tételt [2],
amelyet a Püthagorász-tétel egyféle általánosításának tekintünk.
Tabit
Ibn Korra (826, 901) kitünő arab kommentátor és fordító volt, aki a lefordított
művekbeli bizonyításokat kiegészítette és a tételek egy részét általánosította [2].
A neki tulajdonított tétel felismeréséhez csak a hasonlóság ismeretére volt és
van szükség.
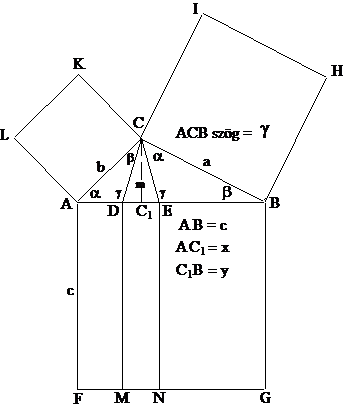
1.
ábra.
A
C csúcsánál tompaszögű ABC háromszög a, b és c oldalaihoz rajzoljunk a, b
illetve c oldalú négyzeteket (lásd az 1. ábrát), majd a háromszög C csúcsánál
lévő g
szögnél szerkesszük be a rajz szerint feltüntetett a
és b
szögeket is. Könnyű belátni, hogy az így kapott CDE háromszög egyenlő szárú,
amelynek magasságát m, a magasság talppontját pedig C1 jelöli.
További jelölések: AC1 = x = b×cos a, C1B = y = a×cos
b
és m = b×sin
a
= a×sin
b.
Az ábráról az is látható, hogy az MNED téglalap területe egyenlő a DE×c
szorzattal (EN = AB = c). Megmutatjuk, hogy az MNED téglalap területe éppen -2×a×b×cosg
(0 <
g
<
180).
A
Tabit-tétel az 1. ábrán látható - itt didaktikai okok miatt C csúcsánál
tompaszögű - háromszög jelöléseivel kimondja, hogy:
BC2
+ CA2 = AD×DM
+ EB×BG
= AB×(AD
+ EB), (DM = BG = AB = c). (1)
Ugyanez más jelölésekkel és másképpen is
felírva:
a2
+ b2 = AD×c
+ EB×c
= c2 - DE×c,
amelyből
c2
= a2 + b2 + DE×c
(2)
adódik. Itt a DE×c
szorzat az MNED téglalap területe. Ha Tabit mester ezt a területet - »1100
évvel ezelőtt - kiszámolta volna, akkor a koszinusz-tétel felismerését neki is
megköszönhetnénk. Ennek bemutatására - már a mai ismereteinkkel - számoljuk ki
az MNED téglalap területét! Az 1. ábrán látható BC = a, AC = b, AB = c = AF, b×cosa
= AC1 = x, a×cosb
= C1B = y, m = a×sinb
= b×sina
és ACB szög = g jelöléseket használva a Tabit mester által ki
nem számolt MNED téglalap területére
DE×c = c2 - a2 - b2
= (x + y)2 - a2 - b2 = 2×x×y
- (a2 - y2) - (b2 - x2) =
= 2×x×y - m2 - m2 = 2×(x×y
- m2) = 2×(b×cosa
×
a×cosb
- b×sina
×
a×sinb)
=
= 2×a×b×(cosa×cosb
- sina×sinb)
= 2×a×b×cos(a+b)
= -2×a×b×cos(180 - (a+b))
=
= -2×a×b×cosg
adódik. Ezt (2)-be írva megkapjuk a
koszinusz-tétel mai alakját:
c2
= a2 + b2 - 2×a×b×cosg.
Ezen törvény a Tabit-tételnél egy kicsivel
többet állít: a g
szög nagyságától függően (0 <
g
<
180) megmondja, hogy az a2 + b2 összeget mekkora értékkel
kell módosítani ahhoz, hogy c2-et kapjunk.
Ha
ezen a késői felismerésen Tabit mester már nem csodálkozhat, csodálkozzunk el
mi azon, amit végül is megsejtett, illetve elkezdett;
de az akkori hiányos ismeretek miatt nem fejezhetett be.
A
Tabit-tétel bizonyítása
Az
1. ábráról megállapítható, hogy az ABC háromszög hasonló az EBC háromszöghöz,
ezért felírható:
AB
: BC = BC : EB, Þ BC2 = AB×EB.
Az ABC háromszög hasonló az ADC háromszöghöz
is, ezért felírható:
AB
: AC = AC : AD, Þ AC2 = AB×AD.
A két egyenlet összeadásával következik:
BC2
+ AC2 = AB×(AD
+ EB),
amely azonos (1)-el.
Irodalom
[1]
Filep L.: A tudományok királynője, 1997, TYPOTEX Kft. - Budapest, Bessenyei
Kiadó - Nyíregyháza, ISBN 963 7546 83 9.
[2]
Lévárdi L. és Sain M.: Matematikatörténeti feladatok, Tankönyvkiadó, Budapest,
1982, ISBN 963 17 6160 6, pp. 114-115.
Szeged, 2003. október 25. Dr. habil.
Ringler András Ph.D.
egyetemi docens