Könyvünk a sokváltozós adatelemzés iránt érdeklődő diákokhoz és szakemberekhez szól. Bár a szerzők szakterülete elsősorban a kémia és a vegyészmérnökség, a könyvet mások is haszonnal forgathatják. Kémikus szemmel nézve a sokváltozós adatelemzés a kemometria tudományágnak az egyik, talán a legnagyobb fejezete. Az itt használt matematikai és számítástechnikai módszerek zömét azonban sok más szakmában is alkalmazzák és folyamatosan fejlesztik.

A bevezetés célja, hogy rávezessen a sokváltozós adatelemzés fogalmaira. A könyv későbbi fejezetei pontosítják majd e fogalmakat; itt még csak az intuitív megértésre támaszkodunk.

A kémiával, más természettudományokkal, mérnöki tudományokkal vagy közgazdaságtannal foglalkozó szakemberek egyre többször találkoznak olyan problémákkal, amelyeket a sokváltozós adatelemzés módszerével kell megoldani. Ennek egyik oka, hogy a számítógépek korában egy-egy dologról, rendszerről (általános kifejezéssel: objektumról) rengeteg adat mérésére és regisztrálására van lehetőség. Ha ráadásul sok objektumról (vagy ugyanarról az objektumról sokszor, de változó körülmények között) gyűjtünk adatokat összehasonlítás, elemzés céljából, akkor az ember számára már áttekinthetetlen adattömeget kapunk, melynek értelmezése, hasznosítása csak számítógépek felhasználásával lehetséges.

A sokváltozós összefüggések és a nagy adathalmazok kezelésének problematikája más szemléletet kíván, mint amihez a természettudományos kutatók, különösen a vegyészek hozzászoktak. A vegyészek egy tipikus kérdésfeltevése: hogyan hat egy reakcióban az A reagens kezdeti koncentrációja a kitermelésre? Természetesen a kitermelésre sok minden hat, például a többi reagens kezdeti koncentrációja, a reakcióelegy hőmérsékletének szabályozása stb. Más szóval a vizsgált célfüggvény (a kitermelés) több változótól is függ. Többváltozós függvénynél általábannincs értelme megkérdezni, hogy a célfüggvény értékét hogyan befolyásolják külön-külön az egyes változók. Az egyes változók hatása ugyanis függhet a többi változó aktuális értékétől. Például ha a z célfüggvény az x és y változóktól

z = 3xy

függvénykapcsolat szerint függ, akkor az x-től való függést leíró egyenlet

z = 0       (ha y = 0)
z = 3x     (ha y = 1)
z = 12x   (ha y = 4)

és így tovább. Vannak viszont esetek, amikor érdemes külön foglalkozni az egyes változók hatásával, pl. ha

z = 3x² + 5 lg y.

Bár z értéke itt is mindkét változótól függ, változásában jól el lehet különíteni x és y hatását. Mindez lehet, hogy triviálisnak tűnik, de az a tény, hogy a kémiaoktatás nehezen tud megszabadulni az ideális gáztörvény Gay–Lussac- és Boyle–Mariotte-törvényre való fölösleges, történelmi indíttatású felbontásától, jól mutatja, hogy a vegyészek mennyire ragaszkodnak a többváltozós összefüggések (itt: Pv = nRT) egyváltozós függvényekre való felbontásához.

Egy másik szokatlan dolog a vegyész számára a sokváltozós világban, hogy a figyelembe vett változók esetleg (sőt többnyire) nem függetlenek egymástól. Például a kromatográfiában két szomszédos csúcs elválását az

elválasztási tényezővel jellemzik, ahol t₁ és t₂ a két csúcs retenciós ideje, s₁éss₂ pedig az egyes csúcsok szélességét jellemző adat. Ha egy vegyészt megkérdezünk, hogy hogyan függ R a (s₁+s₂) összegtől, valószínűleg rávágja, hogy fordítottan arányos vele. Nos, ez nemcsak hogy nem igaz, de még a kérdésnek sincs értelme. Egyrészt a csúcsszélességek összefüggnek a retenciós időkkel (vagyis ha például t-t megváltoztatjuk, akkor s is megváltozik), másrészt mind t, mind s a beállítható kísérleti változók (oszlopméret, töltet, eluens, hőmérséklet, nyomásesés) bonyolult függvénye. (Ha pl. t-t 10 percről 12 percre növeljük, akkor nem mindegy, hogy ezt a térfogatáram csökkentésével vagy az oszlop hosszának növelésével értük el, ugyanis a két esetben s egészen másképp változik). Ez a példa arra is rávilágít, hogy milyen félreértésekhez vezethet, ha fontos változókat kihagyunk a vizsgálatból.

További szokatlan élmény a vegyész számára, hogy a vizsgált változók közti összefüggések esetenként nagyon bizonytalanok. Megszoktuk, hogy ha pl. x, y és z mért adatok és

z = 3xy

összefüggés áll fenn közöttük, akkor x = 2,00 és y = 5,00 esetén z nagyon jó közelítésben 30,0 legyen. Egy-két százalék hibát még csak elviselünk, de 20 százalékot is meghaladó ingadozások esetén súlyos kísérleti hibára gyanakszunk. Nem minden szakma van így ezzel. A biológust aligha lepi meg, ha azt tapasztalja, hogy a felnőtt nyulak fülének hossza az egyedek közt több mint 20%-ot ingadozik. Ennek ellenére ő is (és mi is) értelmesnek tartunk egy olyan vizsgálatot, ahol például ezer különböző életkorú nyúl fülének hosszát megmérik, és összevetik az életkorral. A nagy szórás ellenére is jól ki fog rajzolódni a fülhossz növekedésének trendje.

Az olvasóban most felvetődhet, hogy mindez legyen a biológusok dolga, de a vegyész ilyen bizonytalan adatokkal nem találkozik. Ezen a ponton be kell vallanunk, hogy a vegyészek a sokváltozós adatelemzést többnyire olyan problémák vizsgálatára használják, amelyek a kémiai tananyagban nem szerepelnek, de a vegyészek jó része az életben mégis találkozik velük. A gyakorlatban ugyanis sokszor szembesülünk olyan rendszerekkel, amelyekről sok adatunk van (vagy szerezhető), de amelyeknek a működését nem tudjuk szabatosan leírni. Ilyenek például a környezetvédelmi problémák, a bonyolult technológiák, sok biotechnológiai feladat (pl. szennyvíztisztítás, sajtgyártás), de ilyen például a tömegspektrométerben végbemenő fragmentáció függése a molekulaszerkezettől vagy a molekulaszerkezet függése az infravörös spektrumtól (nem tévedés, itt az analitikai kémiai problémára gondolunk, amikor a spektrum ismert, és ebből kell kitalálni, hogy mi a molekula). Az ilyen összetett problémák általában nem oldhatók meg egy lépésben. Először végiggondoljuk a dolgot, megpróbálunk összefüggéseket találni. Ez az a fázis, ahol különösen jól jönnek a sokváltozós adatelemzési módszerek.

A bonyolult rendszerek viselkedéséről történő adatgyűjtés is többnyire más, mint amit a vegyész megszokott. Laboratóriumi kísérleteinknek legalább a kiindulási állapotát és gyakran a lefutásuk körülményeit (pl. hőmérséklet, nyomás) is mi szabjuk meg. Ha viszont például egy szennyvíztisztító telepen észreveszik, hogy a tisztítás hatásfoka időnként nagyon leromlik, és ezért a megelőző egy év vízvizsgálati és technológiai adatait akarják kielemezni, akkor minden adat úgy adott, ahogy van. Ennek számos lényegbevágó következménye lehet. Például könnyű az adatok közt észrevett összefüggéseket ok-okozati összefüggésként félreértelmezni. A víztisztító mű esetében például lehet, hogy észrevesszük, hogy az üzemzavar előtt mindig megugrott a bejövő szennyvíz Na⁺-koncentrációja. Laikusként azt hihetnénk, hogy az üzemzavart ez okozta. Józan ésszel persze rá fogunk jönni, hogy a közeli gyár ilyenkor engedte le az addig gyűjtögetett szennyvizét, amiben a Na⁺ mellett sok minden más is volt, és a biológiai tisztítást végző mikroorganizmusokra inkább az utóbbiak hatottak, mintsem a nátriumion. A példa azt mutatja, hogy az adatok összefüggésének interpretálásához sokféle szakmai, helyismereti és egyéb információra is szükség lehet.

A sokféle összetartozó adat gyűjtésének számos oka lehet. Ilyen volt a fenti példában az üzemmenet ellenőrzési lehetősége. Lehet a cél jövőbeni anomáliák (kiugró értékek) észlelése is. Így például a Tisza vízösszetételének és vízhozamának folyamatos monitorozása segíthet a szennyezések levonulásának észlelésében. E példában látszólag nincs jelentősége több változó együttes mérésének: ha például cianidszennyeződéstől tartunk, akkor azt kell monitorozni. Sok olyan eset van azonban, amikor egy nem mért komponens jelenlétét is elárulják a mért paraméterek együttes megváltozásai.

Az adatgyűjtés célja lehet technológiák javítása is. Az ipari (pl. vegyipari, élelmiszer-ipari) folyamatokat általában sok paraméter befolyásolja, így a bejövő nyersanya-gok összetétele, a technológiai folyamat beállított paraméterei és esetleg külső tényezők, pl. a levegő páratartalma. Az illető technológiával előállított terméknek is számos fontos tulajdonsága lehet (pl. ha a termék sajt, annak zsírtartalma, lukacsossága, íze stb.). Szakaszos gyártás esetén az egyes sarzsok leírhatók a gyártás bemenő paramétereivel (nyersanyag, technológia) és kimenő paramétereivel (termékjellemzők). Tegyük fel, hogy szeretnénk a sajt relatív lyuktérfogatát valamilyen kívánt értékre beállítani, méghozzá úgy, hogy a zsírtartalom és az íz előírt határok közt maradjanak. Mit és hogyan változtassunk a sok bemenő paraméter közül? A kísérletezés túl drága, ezért inkább a múltbeli sarzsok adataiból próbálunk kiindulni. Minden sarzs legyártása felfogható mint egy vektor-vektor hozzárendelés: a bemenő adatok vektorához hozzárendeljük az adott sarzs kimeneti adatainak vektorát. Erről a leképezésről (függvényről) annyi mintánk (azaz összetartozó bemenő-kimenő vektorpárunk) van, ahány korábbi sarzsot vizsgálunk. Kérdés: hogyan változtassuk meg a bemenő vektort, hogy a kimenő vektor (vagyis a sajt termékjellemzőinek együttese) egy általunk megadott értéket vegyen fel, vagy hogy az általunk megadott tartományba essék? Ha ismernénk az

y = f(x)

függvényt, ahol x a bemenő és y a kimenő adatok vektora, akkor a kívánt y* kimenethez tartozó x* bemenő vektor értéket megpróbálhatnánk meghatározni. (Megjegyzés: nem biztos, hogy volna ilyen x*, és ha volna is, akkor sem biztos, hogy csak egy volna.) Mi azonban nem ismerjük az f függvényt, csak bizonyos számú összetartozó (x, y) párt. Egyváltozós esetben ilyen lenne a helyzet:

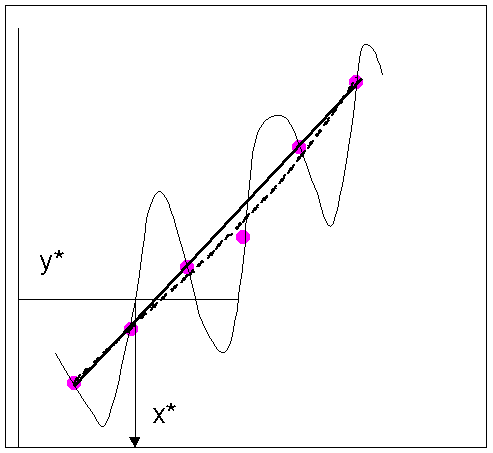
1. ábra

Az ábrán körök jelölik a korábbi sarzsok adatait és megjelöltük a beállítani kívánt y* értéket. A meglévő pontokra illesztett görbéről x* értéke(i) leolvasható(k). Csakhogy a meglévő pontokra sokféleképpen lehet görbét illeszteni. A pontozott (vékony vonalú) görbe minden ponton átmegy, de összevissza ugrál; a szaggatott vonallal rajzolt görbe majdnem minden ponthoz elég közel megy, és elég sima is; a folytonos  (vastag vonalú) görbe még simább, de kihagyja az egyik pontot, mert azt kiugró adatként fogtuk fel. Melyik görbét fogadjuk el? Szakmai tapasztalataink az súgják, hogy a nagyon ugráló görbe aligha az igazi (szaknyelven szólva: túlillesztett). A másik kettő közt azonban nem tudunk dönteni.

Ha x és y többdimenziós vektorok, a helyzet bonyolultabb. Először is szólnunk kell a dimenziók átkáról. Mit takar ez a különös megnevezés? Azt, hogy a dimen-ziók számának növekedtével rohamosan romlik az esélyünk arra, hogy a változók vizsgálni kívánt tartományát ésszerű számú kísérleti ponttal viszonylag sűrűn lefedjük. Az előbbi ábrán a lefedett tartományban 6 pont állt rendelkezésünkre, mégis problémát jelentett a görbeillesztés. Ha x háromdimenziós vektor és mindhárom változó vizsgálandó tartományában 6 osztópontot akarunk elhelyezni, akkor ez a 3-dimenziós x-ek terében 6 ´ 6 ´ 6= 216 kísérleti pontot jelent! Tíz változó esetén 6¹⁰(vagyis több mint hatvanmillió) kísérleti pont kellene a hasonló felbontáshoz. A gyakorlatban erről rendszerint szó sem lehet, tehát a vizsgált tartományban csak nagyon ritkásan lesznek a pontjaink. Ráadásul, ha nem egy tervezett kísérletről van szó, a pontok eloszlása az xtérben olyan, amilyen, alkalmasint igen egyenetlen.

A rendelkezésünkre álló pontoknak ez az egyenetlen eloszlása nagyon hasznos is lehet. Gyakran tapasztalható az, hogy a sokdimenziós ponthalmaz szinte minden pontja benne van egy lényegesen alacsonyabb dimenziójú, sík vagy hajlított “lemezben”. Például, ha minden objektumot három adat jellemez, azaz a pontjaink a háromdimenziós térben vannak, de a három változó közt van valamilyen összefüggés (például: 1 mol ideális gáz esetén P, V és T között: PV= RT), akkor az összes pont egy háromdimenziós térbeli, vastagság nélküli felületen helyezkedik el. Ha a mérések hibával terheltek, vagy ha az összefüggés csak statisztikus (vagyis körülötte kisebb, nem mérési hibából adódó ingadozások is lehetnek), akkor a pontok az “elméleti” felület mentén, egy vastagsággal is rendelkező “lemezben” helyezkednek el. Gyakran fordul elő, hogy ez az effektív dimenziócsökkenés (a változók számáról a lemez dimenziójára) igen nagy; sokszor már egy kétdimenziós síkra illeszkedő lemez is elég az összes pont befoglalására. A pontokat a lemez felületére (vagy inkább középsíkjára) merőlegesen rávetítve végül is a pontok eloszlását kétdimenziós ábrán nézhetjük meg.

A pontok egyenetlen eloszlása adódhat azonban más okból is, mint abból, hogy a változók közt összefüggések vannak. Például lehet, hogy a “mintavételezés” volt torz, vagyis a vizsgálatba bevont pontok térbeli elrendeződése nem követi az összes vizsgálható pont térbeli elrendeződését, a minta tehát nem jellemző a mintázott rendszerre.

Fentebb, a grafikus görbeillesztési probléma kapcsán futólag említettük, hogy a függvényillesztésnél a nem tökéletesen illeszkedő, de egyszerűbb, simább lefutású görbét előnyben részesítjük a tökéletesen illeszkedő, de vadul ingadozóval szemben. Ennek oka, hogy a simább függvények prediktív ereje általában jobb. Ezen azt értjük, hogy ha az adott rendszerből (például: sajtüzem) újabb sarzsok adatait gyűjtjük majd be, azok is illeszkedni fognak a simább görbére, míg a vadul hullámzóra nem. Hogyan lehetne már az eredetileg rendelkezésre álló adatokból is ellenőrizni, hogy jó görbét illesztettünk-e? Erre gyakran használt módszer, hogy az eredeti adatokat véletlenszerű kiválasztással 3 csoportra osztjuk, nagyjából 50:25:25 százalékos arányban; az első csoport alapján illesztjük az egyes használni kívánt modelleket, a másodikon ellenőrizzük, hogy az egyes modellek mennyire alkalmasak előrejelzésre, így kiválasztjuk a legjobb modellt, és végül a harmadik adatcsoport segítségével megvizsgáljuk a kiválasztott legjobb modell használhatóságát “új” (vagyis az illesztés során még ismeretlen) adatokra.

A módszer jó előrejelző képességét valószínűsíti, ha a változók közt feltárt összefüggések nem csak egy pontos, de semmitmondó formulára vezetnek, hanem egy a szakmai tudásunk alapján jól interpretálható, egyszerű szabályosság megfogalmazását teszik lehetővé. Az ilyen eredményt még akkor is előnyben részesítjük, ha a kedvéért néhány kisebb, de statisztikailag szignifikáns effektust el kell hanyagolni. (Statisztikai fogalmazással: kis determinisztikus effektusokat zajként kezelünk és ezzel a becslést torzítjuk, viszont robusztusabbá tesszük.)

Az eddig sorra vett példáink egy részében valamilyen adott bemenő adatvektorhoz ismert kimenő adat vagy adatok tartoztak bizonyos számú objektumra vagy rendszerre vonatkozóan, és ezen minták alapján próbáltunk előrejelzésre (tehát tetszőleges további bemenő adatból a hozzá tartozó kimenő adat számítására) is alkalmas függvényt illeszteni az ismert pontokra. Ennek az úgynevezett regressziós problémának sokféle megoldása ismert, például nem szükséges a teljes vizsgált tartományban egyetlen függvénnyel közelíteni, hanem lehet résztartományonként más függvényt használni (alkalmasint gondoskodva a tartományok határán a sima csatlakozásról). Sőt mi több, nem kell feltétlenül függvényt sem illeszteni, hanem például egy x bemenethez becsülhetjük az y kimenet értékét úgy, hogy az x-hez közeli, már ismert pontokhoz tartozó y értékeket megfelelő súlyozással átlagoljuk. Ez egy úgynevezett nemparaméteres regressziós módszer.

Az adatok lehetnek folytonos változók egyes megvalósult értékei, de lehetnek köztük eleve diszkrétek, sőt számszerűen nem is feltétlenül jellemezhető minőségi, osztályba sorolási adatok is. Így például egy élelmiszertermék ötféle mért jellemzőjét összevethetjük az érzékszervi vizsgálat “megfelelt” – “nem felelt meg” kategorizálási eredményével. Ha a mért jellemzők erre alkalmasak és ha elég sok ismert mintánk volt, akkor újabb minták esetén a mért ötféle adatból előre jelezhetjük az érzékszervi vizsgálat eredményét.

Az előbbi példa alapján felvetődhet bennünk a kérdés: vajon ha az egyes minták öt mért tulajdonságát egy ötdimenziós derékszögű koordináta-rendszerben ábrázoljuk, vagyis minden mintának egy ötdimenziós pont felel meg, nem kell-e a “megfelelt” minősítésű minták pontjainak élesen elkülönülniük a “nem megfelelt” minták pontjaitól? Az alábbi (csak kétváltozós esetet szemléltető) ábra mutatja, hogy esetenként ez így lehet, de nem szükséges, hogy így legyen:
 
 

a)	b)
c)	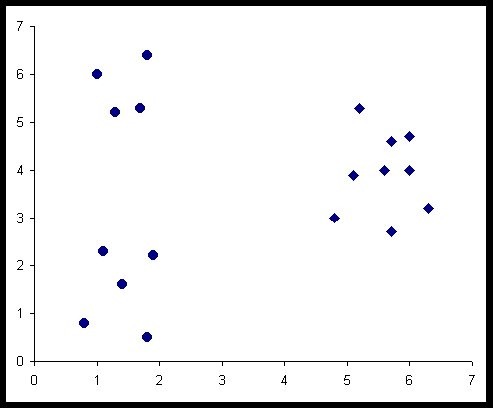d)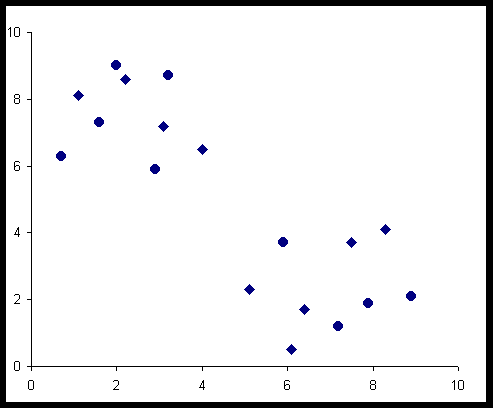

2. ábra
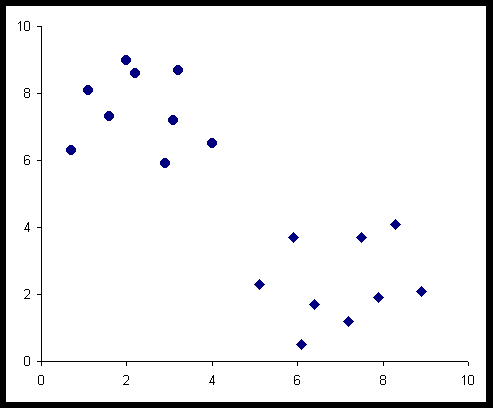
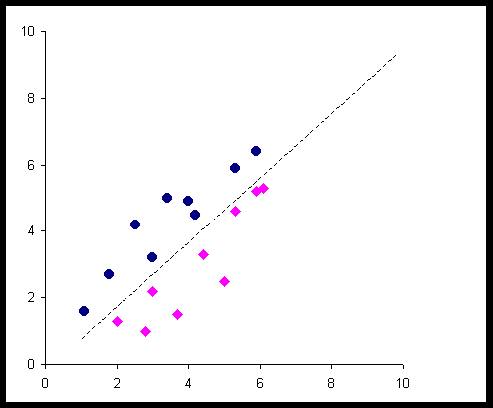
Az ábrákon a kör szimbólum jelentése: "megfelelt", a négyszögé : "nem felelt meg"

Az a) esetben világosan elkülönül a két ponthalmaz és éppen a jó és rossz pontokra. A b) esetben nem vennénk észre az elkülöníthetőséget, ha az érzékszervi minősítés eredménye nem lenne jelölve. A c) esetben három pontcsoport van, ezért ha a minősítést nem ismernénk, itt sem tudnánk az osztályozást elvégezni. A d) esetben a pontok világosan elkülönülnek két csoportra, de az elkülönülésnek nincs köze a minősítéshez.

Ez a négy ábra rámutat arra, hogy csak megfelelően választott tulajdonságok esetén kaphatunk két, egymástól jól elkülönülő, olyan csoportot, amelyek éppen egybeesnek a jó illetve rossz termékek csoportjával. A b) példához azonban érdemes még egyszer visszatérnünk. Mi lett volna, ha az ábrázolt pontoknak csak az x₁ vagy x₂ koordinátáját ismerjük? Vetítsük gondolatban a pontokat merőlegesen csak az x₁ vagy csak az x₂ tengelyre. Az egyes tengelyeken a kétféle pontcsoport teljesen összekeveredik. A példa azt mutatja, hogy érdemes lehet a változók számát növelni a jobb elválasztás érdekében (még akkor is, ha az új változó mentén sincs elkülönülés!).

Ez a példasor elvezetett minket egy újabb témakörhöz: sokdimenziós ponthalmazokon a bemenő és kimenő adatok kijelölése nélkül is lehet összefüggéseket keresni. A fenti példasor a) és d) esetében például rögtön észrevesszük, hogy a pontok két különálló, önmagában koherens csoportra esnek szét (csak a d) esetben a két csoport nem tükrözi a termék elfogadhatóságát). Az összefüggések azonban lehetnek kevésbé nyilvánvalók is. Például lehetséges, hogy az ötdimenziós tér általunk vizsgált pontjai gyakorlatilag mind egy négydimenziós hipersíkra esnek. Ezt nehéz vizuálisan elképzelni, de a helyzet analóg azzal, amikor egy kétdimenziós síkban egy ponthalmaz szinte tökéletesen egy egyenesre esik. Míg a síkbeli esetnél ez azt jelenti, hogy egy pont x₁ értékéből a felismert összefüggés alapján x₂ elég jól megbecsülhető, az ötdimenziós példában x₁, x₂, x₃, x₄ és x₅ közül négyet kell ismerni, hogy az ötödiket megbecsülhessük. Ha pl. csak x₁ értéke ismert, akkor csak annyit tudunk, hogy a többi változók között van egy lineáris összefüggés. Ez a példa azt mutatja, hogy sokváltozós esetben az összefüggések jellege sokkal változatosabb lehet, mint a megszokott egyváltozós esetben.

Ponthalmazok összefüggéseinek, mintázatainak (pattern) felismerésében (recognition) az emberi képességek csodálatosak, de csak alacsony dimenziókban működnek. Ezért a sokváltozós adatelemzésben előszeretettel alkalmazunk olyan technikákat, amelyekkel két vagy három dimenzióban láthatóvá tehető a többdimenziós ponthalmaz elhelyezkedése. Amikor a dimenziók átkáról volt szó, már említettük, hogy sokszor a pontok (éppen a változók között fennálló összefüggések miatt) egy elég alacsony dimenziójú “lemezben” helyezkednek el. Alacsony dimenzióba való leképezések azonban akkor is lehetségesek, ha a pontfelhő még közelítően sem “lapos”. Például a földgömb felületén lévő városok pontjait merőlegesen rávetíthetjük az északi és a déli sarkot összekötő egyenesre. A vetületen jól fog látszani, hogy Fokváros jóval messzebb van Budapesttől, mint Kairó. Viszont Chicago egészen közel esik ezen a vetületen Budapesthez, ami nyilván durva torzítása a gömbfelszíni távolságviszonyoknak. A leképezések tehát torzítanak is, ezért alaposan át kell gondolni a vizuális információkból levont következtetéseket.

Miről szól végül is ez a tankönyv? Az adott terjedelmi korlátok között nem lehetett vállalkozni sem a kemometria, sem a sokváltozós adatelemzés átfogó ismertetésére. Ezért megpróbáltuk kiválogatni azokat a témákat, amelyekre e két témakör átfedő részében a vegyésznek leginkább szüksége lehet. Mivel mindkét szakterület gyorsan fejlődik, igyekeztünk aktuális ismereteket nyújtani, ami viszont korlátokat állított az egyes témák bővebb, több számpéldával segített kifejtése elé. Arra számítunk, hogy azok a tanártársaink, akik a könyvet az oktatásban használják, előadásaik során kiegészítik majd az anyagot saját példáikkal.

Könyvünk megírásakor igyekeztünk figyelembe venni a vegyészhallgatók (kb. harmadik évfolyamtól) és diplomások előzetes ismereteit. Ezek az ismeretek nagyon eltérnek a sokváltozós adatelemzést alkalmazó más szakmabeli kollégákéitól, pl. az informatikusokéitól, a villamosmérnökökéitől, statisztikusokéitól, közgazdászokéitól, biológusokéitól. A kívülálló számára így valószínűleg meglepő lesz, hogy egyes témákba részletesen belemegyünk, másutt csak emlékeztetünk az előismeretekre (pl. mátrixok, lineáris algebra), megint másokat (például a sztochasztikus folyamatokat) pedig csak fogalomismertetési szinten tárgyalunk. Tekintve, hogy még a vegyészek és a vegyészmérnökök ismeretei is elég eltérőek, biztosak vagyunk benne, hogy tanár kollégáink diákjaik igényeinek megfelelően fogják majd módosítani a tárgyalás súlypontjait.

Figyelmeztetni szeretnénk diákot és tanárt egyaránt a szakterületen használt elnevezések problémáira. A könyvben tárgyalt módszereket eredetileg nagyon eltérő szakmákban használták és ezért gyakori, hogy egy-egy módszernek, fogalomnak több neve is van, és hogy e nevek a kémikusok számára nem túl kifejezőek. Könyvünkben igyekeztünk – nem kevés vita árán – minél több angol kifejezésnek szemléletes magyar megfelelőt választani. A legfontosabb magyar szakkifejezéseket azok angol megfelelőivel párba állítva külön is kigyűjtöttük a könyv végén.

Fogalmi zavarokat ebben a szakmában nem csak a megnevezések okoznak, hanem az is, hogy egyes számítási módszerek, algoritmusok fogalma keveredik az adott módszer felhasználási területeinek fogalmával. Gyakoriak a kombinált módszerek is, például a főkomponens-elemzést a legváltozatosabb eljárásokban használják kezdő lépésként.

A kezdő számára gondokat okozhat a matematikai statisztikai szemléletmód követése is. A statisztika a vizsgált adatok véletlenszerű ingadozásaira koncentrál, míg a kémia inkább a determinisztikus jelenségekre. A statisztika sok fontos alkalmazási területén (pl. gazdaság, biológia, pszichológia) a fő kérdés rendszerint az, hogy van-e egyáltalán összefüggés bizonyos nagy szórású változók között. Ilyen szituációban, ha van is összefüggés, aligha érdemes annak pontos függvényalakot keresni, ezért megelégszenek a függvénykapcsolat lineáris közelítésével.

Már említettük, hogy a vegyész számára szokatlan, hogy pl. két változó kapcsolata ennyire laza legyen. Még furcsább azonban, hogy a statisztikus egy spektrofotometriai kalibrációs görbét is mint két valószínűségű változó összefüggését fogja fel. Ebben a szemléletben ugyanis a kalibráló oldatsorozat koncentrációértékei egyetlen “valódi” koncentráció körüli ingadozások eredményének látszanak (ez nem azonos az egyes koncentrációk bemérési, oldatkészítési hibákból adódó kis ingadozásával). A vegyésznek is a statisztikus szemüvegén át kell néznie azonban a kalibráló mintáit olyankor, amikor olyan bonyolult mintákat elemez, amelyekből nem tud tetszőleges összetételt előállítani kalibrációs célra, hanem ehelyett sok (általában természetes eredetű, pl. növényi, állati) mintát fáradságos módszerekkel megelemez, majd az így már ismert összetételű mintákat használja egy egyszerűbb, gyorsabb, de sokváltozós mérési módszerrel (pl. közeli IR spektrum) történő mérésnek a kalibrálására. A statisztikai szemlélet segít a dimenzió redukálásában is. Az a megállapításunk például, hogy a sokváltozós ponthalmazok gyakran egy alacsony dimenziójú “lemezbe” esnek, tulajdonképpen azt jelenti, hogy a pontok szóródása a lemez lapja mentén sokkal nagyobb, mint a lemezre merőlegesen.

Mire lehet használni a könyvünkből megtanulható ismereteket? A kemometria sokváltozós módszerei elsősorban a kémia és a vegyészmérnökség gyakorlati alkalmazásának segédeszközei. Ezért különösen azok számára hasznosak, akik bonyolult gyakorlati problémák megoldásával foglalkoznak. Ugyancsak szükség van ezekre a módszerekre az interdiszciplináris területeken, ahol sok még a bizonytalan, feltáratlan tényező a vizsgált jelenségekben. Végül ismételten hangsúlyozzuk, hogy az itt bemutatandó módszerek nagy részét sok más szakterületen is egyre elterjedtebben használják, így a bioinformatikában, a vállalatvezetésben, a gazdasági elemzésekben, a folyamatirányításban, nagy dokumentum- és adathalmazokban való hatékony keresésnél stb. Mindezek olyan feladatok, amelyekkel a gyakorló vegyész és vegyészmérnök szakmai pályafutása során szinte biztosan találkozik. A kémia egyes modern ágai, pl. a kombinatorikus módszerek, a hatás-szerkezet összefüggések vizsgálata, az NMR spektroszkópia is bőven kínálnak lehetőséget a kemometriai módszerek alkalmazására.

Hogyan lehet alkalmazni adott problémára a könyvből tanultakat? Először is magát a problémát és az elérendő célt kell megfogalmazni. Ezután a 3. ábrán látható séma szerint célszerű dolgozni.

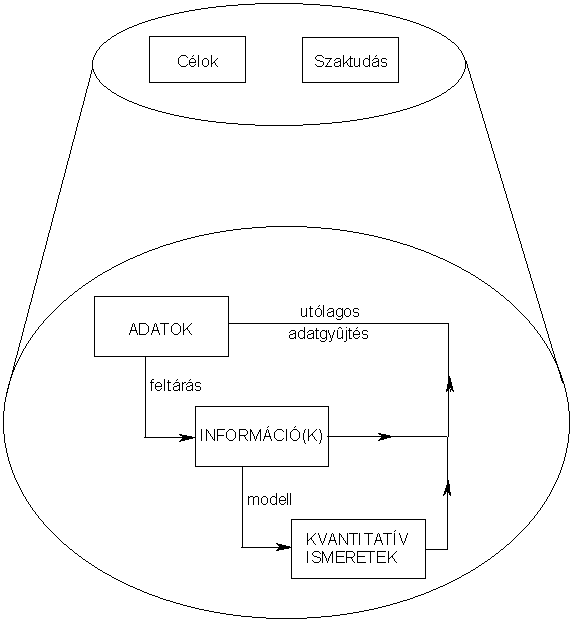
3. ábra

Az első lépés az adatgyűjtés, amelyet korábbi szakmai tapasztalataink alapján, a kitűzött cél figyelembevételével végzünk. Ezt követi a feltáró adatelemzés, vagyis hasznos információk keresése a gyűjtött adathalmazban. A felismerni vélt összefüggések alapján választunk ki valamilyen modellt a rendszer egészének vagy egyes részleteinek leírására. A modell rendszerint egy olyan matematikai leírás, amelynek a paraméterei még meghatározatlanok. Több, alternatív modell is vizsgálható. Esetleg újabb adatok gyűjtését is hasznosnak találhatjuk, mielőtt a következő lépést megtesszük, ami a modell illesztése (regresszió). Ennek eredményeképpen a rendszer közelítő mennyiségi (kvantitatív) leírását kapjuk meg. Az eredményeket szakmai tudásunk alapján értelmezzük és (általában további, célzott adatgyűjtést követően) ellenőrizzük.

A problémamegoldásnak ezt a nagyon általános sémáját követi könyvünk felépítése is. Az I. részben a feltáró adatelemzéssel foglalkozunk, a II. részt a modellillesztésnek szenteltük, a III. részben pedig a szükséges háttérismeretek felfrissítéséhez, áttekintéséhez adunk segítséget. A könyvet a már említett magyar-angol fogalomtár és a sokváltozós adatelemzésre alkalmas számítógépes programcsomagok ismertetése teszi teljessé.

A könyvben bemutatott sokváltozós adatelemzési módszerek általában matematikai ismeretekre támaszkodnak, de ennek ellenére is előfordulhat, hogy téves következtetésekre vezetnek. Ennek alapvetően két oka lehet. A módszerek egy része (különösen a feltáró elemzésben használatosak közül) heurisztikus, azaz logikusnak tűnik, a gyakorlati alkalmazásban is sokszor bevált, de nem bizonyított, hogy minden esetben helyes eredményt ad. Más módszerek (különösen a matematikai statisztikai eljárások) teljesen bizonyítottak ugyan, de a bizonyítás számos szigorú kikötést tartalmaz. Ha adataink nem tesznek eleget e feltételek bármelyikének, akkor a bizonyítás érvényét veszti. (A II. 1. fejezetben sok példát látunk majd arra, hogy a feltételek kis lazítása esetén mi a helyzet.)

Az imént vázolt bizonytalanságok a gyakorlatban nem feltétlenül jelentenek gondot. Ha például egy termék tulajdonságait akarjuk javítani az előállítási technológia optimálásával, lehet hogy nem találjuk meg pontosan az optimumot, de ez nem baj, ha már így is jelentős javulást érünk el. Más, kevésbé nyilvánvaló esetekben három fontos módszerrel védekezhetünk a súlyos tévedések ellen. Egyrészt az eredményeket össze kell vetnünk az előzetes szakmai várakozásunkkal. Nagyon meglepő eredményt ne fogadjunk el csupán azért, mert matematikai jellegű módszerekkel kaptuk. A másik ellenőrzési mód az, hogy több modellt, többféle számítási algoritmust is alkalmazunk minden lehetséges esetben és összevetjük ezek eredményeit. A harmadik módszer abban áll, hogy a felállított modell hihetőségét további, a modell ismeretében tervezett ellenőrző kísérletekkel, mérésekkel, megfigyelésekkel vetjük össze.

E bevezetésben többször is említettük, hogy a sokváltozós adatelemzésben mi minden szokatlan a vegyész számára. Végül azonban eljutottunk arra a felismerésre, hogy a sokváltozós adatelemzés nagyon hasonlít a kémiára. Megismeréséhez sokat kell tanulni, alkalmazásával szép új eredményeket lehet elérni, módszerei és előrejelzései azonban nem mindig tökéletesek és az óvatosságra éppúgy szükség van, mint a kémiai következtetéseknél.