A geológiában, és különösen a gyakran nagy méretű numerikus adatbázisokkal dolgozó geokémia területén gyakran alkalmazunk különböző osztályozási eljárásokat. Mivel számos esetben a geológiai, geokémiai objektumok természetes hierarchikus csoportstruktúrát alkotnak, az agglomeratív és a divizív hierarchikus cluster analízisek használata a legelterjedtebb. Ezek mindegyike valamely, több dimenziós térben értelmezett hasonlóság (távolság) definíció alapján építkezik, általában valamely rekurzív algoritmust követve.

A cluster analízisek fenti osztályába tartozó, széles körben elterjedt módszerek használhatósága számos esetben geológiai szempontok, vagy matematikai okok miatt kérdéses. Ezen okok közül a fontosabbak az alábbiak:

• A minták (pontok) között értelmezett hasonlóság definíciók clusterekre (ponthalmazokra) való alkalmazhatósága (legtávolabbi, legközelebbi szomszéd, medián, stb.) nem egyértelmű (Anderberg, 1973).
• A csoport magok között köztes - térbeli - helyzetű minták nehezen azonosíthatók (Zahn, 1971). Ez - matematikai megoldatlansága mellett - különösen fontos egyes geológiai problémák (pl. magmás differenciáció) vizsgálata során.
• Az egyes csoportok homogenitásáért, illetve a különböző csoportok közötti heterogenitásért felelős változók az alkalmazott osztályozó algoritmussal általában nem vizsgálhatók. Erre lényegesen eltérő filozófiájú eljárásokat (pl. diszkriminancia analízis) kell használni.
• Az egymást követő, eltérő körülmények között lezajló geológiai folyamatok a kémiai (fizikai, ásványtani, stb.) paraméterek más-más körét érintették. Így a pillanatnyi többváltozós csoportstruktúra mindezen hatásokat együtt mutatva gyakran nehezen értelmezhető.

1. Minden változóra definiáljunk egy egydimenziós hasonlóságot (legegyszerűbb esetben különbségük abszolút értékét). Adjunk meg változónként egy-egy küszöbértéket, amely alatt a hasonlóságot szignifikánsnak tekintjük. (A gyakorlatban jól bevált az i*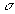/n definíció, ahol i 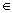N; i a hasonlósági küszöb - “similarity level”.)
2. A hagyományos adat mátrixból (n minta, m változó) a fenti küszöbérték, mint indikátor függvény alkalmazásával m darab, n*n típusú dichotom hasonlóság mátrix származtatható (A_i).
3. Képezzük az A=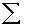A_i mátrixot, amely többváltozós hasonlóság mátrixként értelmezhető. A(i,j) az i és j mintákban hasonló változók száma.
4. Az A mátrixban egymáshoz adott számú változóban hasonló minták csoportot alkotnak. Ezen szám (kapcsolódási küszöb - “connection level”) lépésenkénti csökkentése vagy növelése hierarchikus csoportstruktúrát definiál.

A bevezetett eljárás legfontosabb tulajdonságai az alábbiak:

• Hierarchikus osztályozás, amely sem nem agglomeratív, sem nem divizív. Az eredmény ugyanakkor megjeleníthető könnyen értelmezhető grafikus formában (pl. dendrogram).
• Valódi többdimenziós hasonlóság definíció helyett egydimenziós indikátor függvényeket használ. Valamely két minta távolságát a szignifikánsan hasonló változóik száma definiálja.
• Nem követeli meg a távolságfogalom általánosítását clusterekre.
• A szignifikanciaszint (hasonlósági küszöb) változtatásával számos azonos filozófiájú, egymástól némileg eltérő csoportszerkezet állítható elő. A kiértékelésnél ez alapján a stabilan csoporthoz tartozó, valamint az átmeneti helyzetű minták felismerhetőek.
• Az egyes csoportok elemszáma, valamint a bennük, illetve közöttük előforduló hasonlósági kapcsolatok számának figyelembevételével a változók csoportképző szerepe kvantifikálható. Így 3 mutató (homogenitási, heterogenitási, diszkriminációs index) került bevezetésre:

A bemutatott osztályozó eljáráshoz F77 (Todd, M Tóth, 1999) és Basic nyelven felhasználói szoftverek készültek. A módszert az alábbi kutatások során használtuk eredményesen:

• A Pannon medence kristályos aljzatában található polimetamorf, mállott metabázikus kőzetek geokémiai vizsgálata eltérő premetamorf eredetű vulkanitok ÉÉK-DDNY irányú pásztás elrendeződését bizonyította (Todd, M Tóth, 1999).
• Kérdéses tektonikai helyzetű, eltérő korú amfibolitok geokémiai alapú felismerése a svájci Központi Alpokban.
• Az Alpi orogenezis különböző fázisainak azonosítása monacitok (CePO₄) ritkaföldfém spektruma alapján.
• Az ománi Masirah masszívum bázikus magmatitjainak geokémiai alapú osztályozása.

Bár az itt bemutatott eljárás eredetileg geokémiai problémák megoldására került kidolgozásra, általánossága miatt egyéb osztályozási feladatok során is alkalmazható lehet.

Irodalom

Anderberg, M. R. (1973): Cluster analysis for application. Academic press, 359 p.

M Tóth, T. (1992): Földtani objektumok csoportosítása gráfelmélet segítségével Szeghalmi amfibolitok példáján. Földtani Közlöny, , 122/2-4: 251-263

M Tóth, T., Engi, M. (1997) : A new cluster analysis method for altered rock samples. Schweiz. Mineral. Petrogr. Mitt., 77: 439-447

Todd, C. S., M Tóth, T. (1999): Cluster1 and Cluster2; FORTRAN programs for cluster analysis using graph theory. Comp and Geosci, in press

Zahn, C. T. (1971): Graph-theoretical methods for detecting and describing gestalt clusters. IEEE Transactions on Computers C-20(1), 68-86.